Advertisements
Advertisements
प्रश्न
Form the following figure, find the values of:
- cos B
- tan C
- sin2B + cos2B
- sin B. cos C + cos B. sin C

उत्तर
Given angle BAC = 90°
⇒ BC2 = AB2 + AC2 ...(BC is hypotenuse)
⇒ 172 = 82 + AC2
⇒ AC2 = 289 - 64
⇒ AC2 = 225
⇒ AC = `sqrt225`
∴ AC = 15
(i) cos B = `"base"/"hypotenuse" = "AB"/"BC" = 8/17`
(ii) tan C = `"perpendicular"/"base" = "AB"/"AC" = 8/15`
(iiii) sin B = `"perpendicular"/"hypotenuse" = "AC"/"BC" = 15/17`
cos B = `"base"/"hypotenuse" = "AB"/"BC" = 8/17`
∴ sin2 B+ cos2 B = `(("perpendicular")/("hypotenuse"))^2 + (("base")/("hypotenuse"))^2`
= ` (15/ 17)^2 + (8 /17)^2`
= `(225 + 64) / (289) `
= `(289)/(289) `
= 1
(iv) sin B = `"perpendicular"/"hypotenuse" = "AC"/"BC" = 15/17`
cos B = `"base"/"hypotenuse" = "AB"/"BC" = 8/17`
sin C = `"perpendicular"/"hypotenuse" = "AB"/"BC" = 8/17`
cos C = `"base"/"hypotenuse" = "AC"/"BC" = 15/17`
sin B · cos C + cos B · sin C
= ` 15/17. 15/17 + 8/17. 8/17 `
= `( 225 + 64 )/ (289)`
= `(289)/(289)`
= 1
APPEARS IN
संबंधित प्रश्न
If cosec θ = `sqrt(10)` find all the values of all T-ratios of θ
If x = cot A + cos A and y = cot A – cos A then prove that `((x-y)/(x+y))^2 + ((x-y)/2)^2=1`
Show that:
(i)` (1-sin 60^0)/(cos 60^0)=(tan60^0-1)/(tan60^0+1)`
If A = 450 , verify that:
(ii) cos 2A = 2 cos2 A – 1 = 1 – 2 sin2 A
In the adjoining figure, ΔABC is right-angled at B and ∠A = 450. If AC = 3`sqrt(2)`cm, find (i) BC, (ii) AB.
From the following figure, find the values of
(i) sin B
(ii) tan C
(iii) sec2 B - tan2B
(iv) sin2C + cos2C
If sin A = `(sqrt3)/(2)` and cos B = `(sqrt3)/(2)` , find the value of : `(tan"A" – tan"B")/(1+tan"A" tan"B")`
If 5 cos = 6 sin ; evaluate:
(i) tan θ
(ii) `(12 sin θ – 3 cos θ)/(12 sin θ + 3 cos θ)`
In the given figure, PQR is a triangle, in which QS ⊥ PR, QS = 3 cm, PS = 4 cm and QR = 12 cm, find the value of: 4sin2R - `(1)/("tan"^2"P")`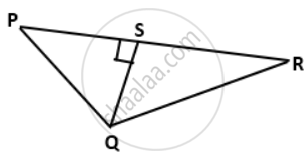
In a right-angled triangle PQR, ∠PQR = 90°, QS ⊥ PR and tan R =`(5)/(12)`, find the value of sin ∠PQS
