Advertisements
Advertisements
प्रश्न
In a right-angled triangle PQR, ∠PQR = 90°, QS ⊥ PR and tan R =`(5)/(12)`, find the value of sin ∠PQS
उत्तर
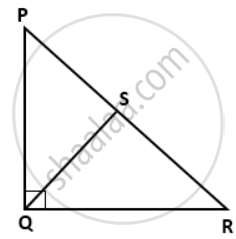
tan R = `(5)/(12)`
⇒ `"PQ"/"QR" = (5)/(12)`
⇒ PQ = 5 and QR = 12
In right-angled ΔPQR,
PR
= PQ2 + QR2
= 52 + 122
= 25 + 144
= 169
⇒ PR = 13
∠PQS + ∠P = 90° and ∠P + ∠R = 90°
⇒ ∠PQS + ∠P = ∠P +∠R
⇒ ∠PQS = ∠R
∴ sin ∠PQS
= sin R
= `"PQ"/"PR"`
= `(5)/(13)`.
APPEARS IN
संबंधित प्रश्न
If `sin A = 9/41` compute cos 𝐴 𝑎𝑛𝑑 tan 𝐴
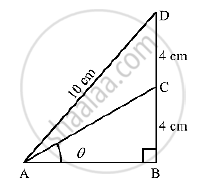
In the adjoining figure, `∠B = 90° , ∠BAC = theta° , BC = CD = 4cm and AD = 10 cm`. find (i) sin theta and (ii) `costheta`
In ΔABC , ∠C = 90° ∠ABC = θ° BC = 21 units . and AB= 29 units. Show thaT `(cos^2 theta - sin^2 theta)=41/841`
Evaluate:
cos600 cos300− sin600 sin300
In the adjoining figure, ΔABC is right-angled at B and ∠A = 450. If AC = 3`sqrt(2)`cm, find (i) BC, (ii) AB.
If 3x = cosecθ = and `3/x= cottheta` find the value of 3`(x^2-1/x^2)`.
Given: sec A = `( 29 )/(21), "evaluate : sin A" - 1/tan "A"`
If 5 cos = 6 sin ; evaluate:
(i) tan θ
(ii) `(12 sin θ – 3 cos θ)/(12 sin θ + 3 cos θ)`
In ΔABC, ∠B = 90°. If AB = 12units and BC = 5units, find: cos C
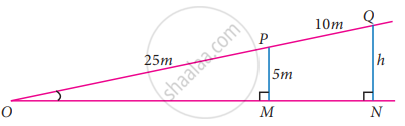
A boy standing at a point O finds his kite flying at a point P with distance OP = 25 m. It is at a height of 5 m from the ground. When the thread is extended by 10 m from P, it reaches a point Q. What will be the height QN of the kite from the ground? (use trigonometric ratios)