Advertisements
Advertisements
प्रश्न
In ΔABC , ∠C = 90° ∠ABC = θ° BC = 21 units . and AB= 29 units. Show thaT `(cos^2 theta - sin^2 theta)=41/841`
उत्तर
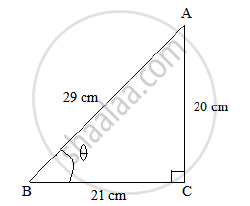
Using Pythagoras theorem, we get:
`AB^2 = AC^2 + BC^2`
`⟹ AC^2 = AB^2 − BC^2`
`⟹ AC^2 = (29)^2 − (21)^2`
`⟹ AC^2 = 841 − 441`
`⟹ AC^2 = 400`
⟹ 𝐴𝐶 = `sqrt(400)` = 20 𝑢𝑛𝑖𝑡𝑠
Now , sin `theta =(AC)/(AB) = (2theta)/29 and cos theta = (BC)/(AB)=21/29`
`cos^2 theta - sin^2 theta = (21/29)^2 - (20/29)^2 = 441/841 - 400/841 = 41/841`
Hence proved.
APPEARS IN
संबंधित प्रश्न
In a ΔABC, right angled at A, if tan C = `sqrt3` , find the value of sin B cos C + cos B sin C.
If A = B = 60°, verify that sin (A − B) = sin A cos B − cos A sin B
Evaluate:
cos450 cos300 + sin450 sin300
If 3x = cosecθ = and `3/x= cottheta` find the value of 3`(x^2-1/x^2)`.
Given: sec A = `( 29 )/(21), "evaluate : sin A" - 1/tan "A"`
If cosec θ = `(29)/(20)`, find the value of: cosec θ - `(1)/("cot" θ)`
From the given figure, find the values of cos C
From the given figure, find the values of tan C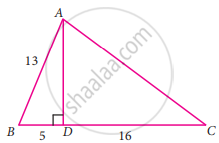
From the given figure, find the values of cosec C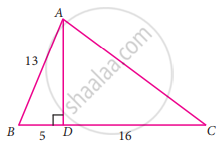
If cos A = `(2x)/(1 + x^2)`, then find the values of sin A and tan A in terms of x
