Advertisements
Advertisements
प्रश्न
Given: sec A = `( 29 )/(21), "evaluate : sin A" - 1/tan "A"`
उत्तर
Consider the diagram below :
sec A = `(29)/(21)`
i.e. `"hypotenuse"/"base" = (29)/(21) ⇒ "AC"/"AB" = (29)/(21)`
Therefore if length of AB = 21x , length of AC = 29x
Since
AB2 + BC2 = AC2 ...[ Using Pythagoras Theorem ]
(21x)2 + BC2 = ( 29x)2
BC2 = 841x2 – 441x2 =400x2
BC = 20x ...(perpendicular )
Now
sin A = `"perpendicular"/"hypotenuse" = (20x)/(29x) = 20/29`
tan A = `"perpendicular"/"base" = (20x)/(21x) = 20/21`
Therefore
sin A – `1/ tan "A"`
= `(20)/(29) – 1/(20/21)`
= `(20)/(29) – 21/20`
= – `(209)/(580)`
APPEARS IN
संबंधित प्रश्न
if `sec A = 5/4` verify that `(3 sin A - 4 sin^3 A)/(4 cos^3 A - 3 cos A) = (3 tan A - tan^3 A)/(1- 3 tan^2 A)`
If cot θ = 2 find all the values of all T-ratios of θ .
If cosec θ = `sqrt(10)` find all the values of all T-ratios of θ
Evaluate:
`4/(cot^2 30^0) +1/(sin^2 30^0) -2 cos^2 45^0 - sin^2 0^0`
If sec A = `sqrt2`, find the value of :
`(3cos^2"A"+5tan^2"A")/(4tan^4"A"–sin^2"A")`
In ΔABC, ∠B = 90°. If AB = 12units and BC = 5units, find: tan A
If 8 tanθ = 15, find (i) sinθ, (ii) cotθ, (iii) sin2θ - cot2θ
In a right-angled triangle PQR, ∠PQR = 90°, QS ⊥ PR and tan R =`(5)/(12)`, find the value of tan ∠SQR
In the given figure, AC = 13cm, BC = 12 cm and ∠B = 90°. Without using tables, find the values of: sin A cos A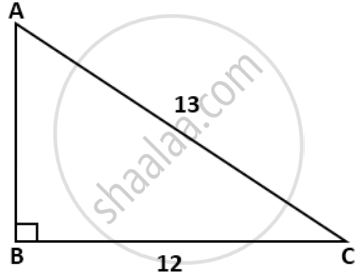
In the given figure, AC = 13cm, BC = 12 cm and ∠B = 90°. Without using tables, find the values of: `("cos A" - "sin A")/("cos A" + "sin A")`