Question

Given: tan A = `4/3 , "find" : ("cosec""A")/(cot "A"– sec "A")`

Answer 1

Consider the diagram below :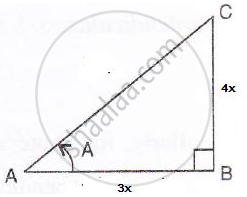

tan A = `(4)/(3)`

i.e. `"perpendicular"/"base" = (4)/(3) ⇒ "BC"/"AB" = (4)/(3)`

Therefore if length of AB = 3x, length of BC = 4x

Since
AB² + BC² = AC²    ... [ Using Pythagoras Theorem ]

( 3x )² + (4x)² = AC²

AC² = 9x² + 16x² = 25x²

AC = 5x                   ...( hypotenuse )

Now

sec A = `" hypotenuse "/"base" = "AC"/"AB" =(5x)/ (3x) = (5)/(3)`

cot A = `" base "/"perpendicular" = "AB"/"BC" = (3x)/ (4x) = (3)/(4)`

cosec A = `" hypotenuse "/"perpendicular" = "AC"/"BC" = (5x)/(4x)  = (5)/(4)`

Therefore

`("cosec""A")/(cot"A" – sec "A")`

= `(5/ 4) /(3/4  – 5/3)`

= ` (5 /4)/(– 11/12)`

= `– (60)/(44) `

= `– (15)/(11)`