Advertisements
Advertisements
प्रश्न
In an isosceles triangle ABC, AB = BC = 6 cm and ∠B = 90°. Find the values of cos C
उत्तर
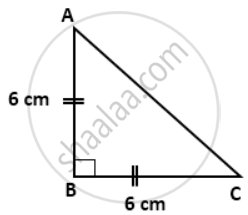
ΔABC is an isosceles right-angled triangle.
∴ AC2
= AB2 + BC2
= 62 + 62
= 36 + 36
= 72
⇒ AC = `6sqrt(2)"cm"`
cos C
= `"BC"/"AC"`
= `(6)/(6sqrt(2)`
= `(1)/sqrt(2)`.
APPEARS IN
संबंधित प्रश्न
If 3 cot A = 4, Check whether `((1-tan^2 A)/(1+tan^2 A)) = cos^2 "A" - sin^2 "A"` or not.
If 8 tan A = 15, find sin A – cos A.
If sec 2A = cosec (A – 42°) where 2A is an acute angle. Find the value of A.
If sin θ = ` (a^2 - b^2)/(a^2+b^2)`find all the values of all T-ratios of θ .
Verify each of the following:
(i)`sin 60^0 cos 30^0-cos 60^0 sin 30^0`
If sin A + cosec A = 2;
Find the value of sin2 A + cosec2 A.
If sec A = `sqrt2` , find : `(3cot^2 "A"+ 2 sin^2 "A")/ (tan^2 "A" – cos ^2 "A")`.
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
cose C = `(15)/(11)`
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
sinB = `sqrt(3)/(2)`
In a right-angled triangle PQR, ∠PQR = 90°, QS ⊥ PR and tan R =`(5)/(12)`, find the value of tan ∠SQR
