Advertisements
Advertisements
प्रश्न
In the given figure, PQR is a triangle, in which QS ⊥ PR, QS = 3 cm, PS = 4 cm and QR = 12 cm, find the value of: 4sin2R - `(1)/("tan"^2"P")`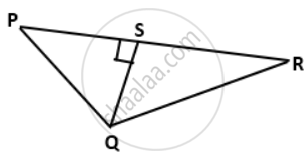
उत्तर
sin R = `"QS"/"QR" = (3)/(12)`
4sin2R - `(1)/("tan"^2"P")`
= 4sin2R - cot2P
= `4 xx (3/12)^2 - ("cos P"/"sin P")^2`
= `4 xx (9)/(144) - ((4/5)/(3/5))^2`
= `(9)/(36) - (16)/(9)`
= `-(55)/(36)`.
APPEARS IN
संबंधित प्रश्न
In ΔPQR, right angled at Q, PQ = 4 cm and RQ = 3 cm. Find the values of sin P, sin R, sec P and sec R.
If A = B = 60°. Verify `tan (A - B) = (tan A - tan B)/(1 + tan tan B)`
If tan θ = `20/21` show that `((1-sin θ + cos θ))/((1+ sin θ +cos θ)) = 3/7`
In ΔABC , ∠C = 90° ∠ABC = θ° BC = 21 units . and AB= 29 units. Show thaT `(cos^2 theta - sin^2 theta)=41/841`
If A = 600 and B = 300, verify that:
(i) sin (A – B) = sin A cos B – cos A sin B
In rectangle ABCD, diagonal BD = 26 cm and cotangent of angle ABD = 1.5. Find the area and the perimeter of the rectangle ABCD.
If 5 cos θ = 3, evaluate : `(co secθ – cot θ)/(co secθ + cot θ)`
In an isosceles triangle ABC, AB = BC = 6 cm and ∠B = 90°. Find the values of cosec C
In the given figure, AD is the median on BC from A. If AD = 8 cm and BC = 12 cm, find the value of tan x. cot y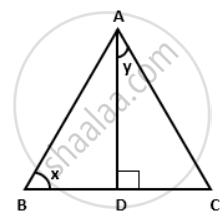
Assertion (A): For 0 < 0 ≤ 90°, cosec θ – cot θ and cosec θ + cot θ are reciprocal of each other.
Reason (R): cot2 θ – cosec2 θ = 1.
