Advertisements
Advertisements
प्रश्न
Assertion (A): For 0 < 0 ≤ 90°, cosec θ – cot θ and cosec θ + cot θ are reciprocal of each other.
Reason (R): cot2 θ – cosec2 θ = 1.
पर्याय
Both Assertion (A) and Reason (R) are true; and Reason (R) is the correct explanation of Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct explanation of Assertion (A).
Assertion (A) is true, but Reason (R) is false.
Assertion (A) is false, but Reason (R) is true.
उत्तर
Assertion (A) is true, but Reason (R) is false.
APPEARS IN
संबंधित प्रश्न
If ∠A and ∠P are acute angles such that tan A = tan P, then show that ∠A = ∠P.
If Sec 4A = cosec (A – 20°) where 4A is an acute angle, find the value of A.
If cot θ = 2 find all the values of all T-ratios of θ .
Evaluate:
`(5 cos^2 60^circ + 4 sec^2 30^circ - tan^2 45^circ)/(sin^2 30^circ + cos^2 30^circ)`
Evaluate:
`2cos^2 60^0+3 sin^2 45^0 - 3 sin^2 30^0 + 2 cos^2 90 ^0`
From the following figure, find the values of
(i) sin B
(ii) tan C
(iii) sec2 B - tan2B
(iv) sin2C + cos2C
In triangle ABC, AB = AC = 15 cm and BC = 18 cm. Find:
- cos B
- sin C
- tan2 B - sec2 B + 2
If sin A = `(7)/(25)`, find the value of : `(2"tanA")/"cot A - sin A"`
In the given figure, AC = 13cm, BC = 12 cm and ∠B = 90°. Without using tables, find the values of: sin A cos A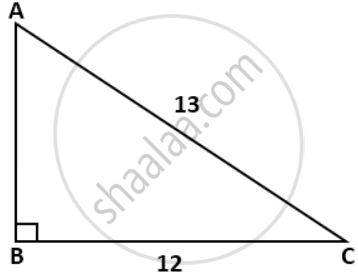
Evaluate: `5/(cot^2 30^circ) + 1/(sin^2 60^circ) - cot^2 45^circ + 2 sin^2 90^circ`.
