Advertisements
Advertisements
प्रश्न
Evaluate: 5 cosec2 45° – 3 sin2 90° + 5 cos 0°.
उत्तर
5 cosec2 45° – 3 sin2 90° + 5 cos 0°
= `5(sqrt(2))^2 - 3(1)^2 + 5(1)`
= 10 – 3 + 5
= 12.
संबंधित प्रश्न
In the following, one of the six trigonometric ratios is given. Find the values of the other trigonometric ratios.
`cot theta = 12/5`
Find the value of x in the following :
`sqrt3 sin x = cos x`
The value of cos 0°. cos 1°. cos 2°. cos 3°… cos 89° cos 90° is ______.
If sin θ + sin² θ = 1, then cos² θ + cos4 θ = ______.
If cos A = `4/5`, then the value of tan A is ______.
If sin A = `1/2`, then the value of cot A is ______.
The value of the expression `[(sin^2 22^circ + sin^2 68^circ)/(cos^2 22^circ + cos^2 68^circ) + sin^2 63^circ + cos 63^circ sin 27^circ]` is ______.
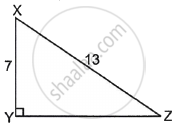
In the given figure, if sin θ = `7/13`, which angle will be θ?
If f(x) = `3cos(x + (5π)/6) - 5sinx + 2`, then maximum value of f(x) is ______.
Evaluate 2 sec2 θ + 3 cosec2 θ – 2 sin θ cos θ if θ = 45°.
