Advertisements
Advertisements
प्रश्न
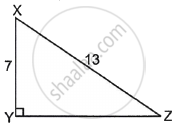
In the given figure, if sin θ = `7/13`, which angle will be θ?
उत्तर
Given: sin θ = `7/13`
According to the trigonometric ratios formula,
sin θ = `"Perpendicular"/"Hypotenuse"`
= `7/13`
Hence, the angle θ is ∠XZY.
APPEARS IN
संबंधित प्रश्न
In ΔABC right angled at B, AB = 24 cm, BC = 7 m. Determine:
sin A, cos A
If sin A = `3/4`, calculate cos A and tan A.
If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠A = ∠B.
Prove that `(sin "A" - 2sin^3 "A")/(2cos^3 "A" - cos "A") = tan "A"`
In the following, trigonometric ratios are given. Find the values of the other trigonometric ratios.
`sin A = 2/3`
If sin θ = `12/13`, Find `(sin^2 θ - cos^2 θ)/(2sin θ cos θ) × 1/(tan^2 θ)`.
if `sec A = 17/8` verify that `(3 - 4sin^2A)/(4 cos^2 A - 3) = (3 - tan^2 A)/(1 - 3 tan^2 A)`
Evaluate the following
`2 sin^2 30^2 - 3 cos^2 45^2 + tan^2 60^@`
Evaluate the Following
`(tan^2 60^@ + 4 cos^2 45^@ + 3 sec^2 30^@ + 5 cos^2 90)/(cosec 30^@ + sec 60^@ - cot^2 30^@)`
Evaluate the Following
`sin 30^2/sin 45^@ + tan 45^@/sec 60^@ - sin 60^@/cot 45^@ - cos 30^@/sin 90^@`
If cos (81 + θ)° = sin`("k"/3 - theta)^circ` where θ is an acute angle, then the value of k is ______.
If x sin (90° – θ) cot (90° – θ) = cos (90° – θ), then x is equal to ______.
The value of the expression (sin 80° – cos 80°) is negative.
A ladder rests against a vertical wall at an inclination α to the horizontal. Its foot is pulled away from the wall through a distance p so that its upper end slides a distance q down the wall and then the ladder makes an angle β to the horizontal. Show that `p/q = (cos β - cos α)/(sin α - sin β)`
Prove that: cot θ + tan θ = cosec θ·sec θ
Proof: L.H.S. = cot θ + tan θ
= `square/square + square/square` ......`[∵ cot θ = square/square, tan θ = square/square]`
= `(square + square)/(square xx square)` .....`[∵ square + square = 1]`
= `1/(square xx square)`
= `1/square xx 1/square`
= cosec θ·sec θ ......`[∵ "cosec" θ = 1/square, sec θ = 1/square]`
= R.H.S.
∴ L.H.S. = R.H.S.
∴ cot θ + tan θ = cosec·sec θ
Let f(x) = sinx.cos3x and g(x) = cosx.sin3x, then the value of `7((f(π/7) + g(π/7))/(g((5π)/14) + f((5π)/14)))` is ______.
Let tan9° = `(1 - sqrt((sqrt(5)k)/m))k` where k = `sqrt(5) + 1` then m is equal to ______.
If θ is an acute angle and sin θ = cos θ, find the value of tan2 θ + cot2 θ – 2.
Evaluate: 5 cosec2 45° – 3 sin2 90° + 5 cos 0°.
