Question

In the following, trigonometric ratios are given. Find the values of the other trigonometric ratios.

`sin A = 2/3`

Answer 1

We know that `sin theta = "opposite side"/"hypotenuse"`

Let us Consider a right-angled ΔABC

 

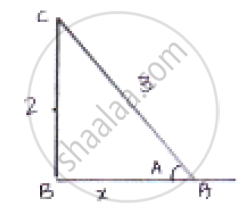
By applying Pythagorean theorem we get

𝐴𝐶² = 𝐴𝐵² + 𝐵𝐶²

`9 = x^2 + 4`

`x = sqrt5`

We know that = `cos = "adjacent side"/"hypotenuse"` and

`tan theta = "opposite side"/"adjacent side"`

So `cos theta  = sqrt5/3`

`sec = 1/cos theta = 3/sqrt5`

`tan theta = 2/sqrt5`

`cot = 1/tan theta =  sqrt5/2`

`cosec theta = 1/ sin theta = 3/2`

Answer 2

Given:    sin` A=2/3`……(1)

By definition

`sin A= "perpendicular"/"Hypotenuse"` …... (2)

By Comparing (1) and (2)

We get,

Perpendicular side = 2 and

Hypotenuse = 3 

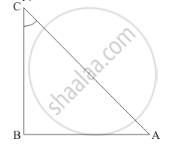
Therefore, by Pythagoras theorem,

`AC^2=AB^2+BC^2`

Now we substitute the value of perpendicular side (BC) and hypotenuse (AC) and get the base side (AB)

Therefore,

`3^2=AB^2+2^2`

`AB^2=3^2-2^2`

`AB^2=9-4`

`AB^2=5`

`AB=sqrt5` 

Hence, Base = `sqrt5` 

Now, `Cos A=" Base"/ "Hypotenuse"`

Cos A=` sqrt 5/3`

Now, `Sec 4= "Hypotenuse"/"Perpendicluar"` 

Therefore,

`"Cosec" A= "Hypotenuse"/"Perpendicular"`

`"Cosec" A=3/2` 

Now, `tan A="Perpendicular"/"Base"`

Therefore,

`Sec A=3/sqrt5`

Now, `tan A "Perpendicular"/"Base"`

Therefore,

`tan A= 2/sqrt5`

Now,`Cos A= "Base"/"Perendicluar"`

Therefore,

`Cot A= sqrt 5/2`