Advertisements
Advertisements
Question
In the following, trigonometric ratios are given. Find the values of the other trigonometric ratios.
`sin A = 2/3`
Solution 1
We know that `sin theta = "opposite side"/"hypotenuse"`
Let us Consider a right-angled ΔABC
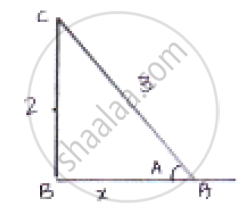
By applying Pythagorean theorem we get
𝐴𝐶2 = 𝐴𝐵2 + 𝐵𝐶2
`9 = x^2 + 4`
`x = sqrt5`
We know that = `cos = "adjacent side"/"hypotenuse"` and
`tan theta = "opposite side"/"adjacent side"`
So `cos theta = sqrt5/3`
`sec = 1/cos theta = 3/sqrt5`
`tan theta = 2/sqrt5`
`cot = 1/tan theta = sqrt5/2`
`cosec theta = 1/ sin theta = 3/2`
Solution 2
Given: sin` A=2/3`……(1)
By definition
`sin A= "perpendicular"/"Hypotenuse"` …... (2)
By Comparing (1) and (2)
We get,
Perpendicular side = 2 and
Hypotenuse = 3
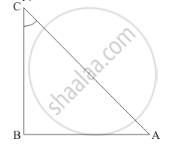
Therefore, by Pythagoras theorem,
`AC^2=AB^2+BC^2`
Now we substitute the value of perpendicular side (BC) and hypotenuse (AC) and get the base side (AB)
Therefore,
`3^2=AB^2+2^2`
`AB^2=3^2-2^2`
`AB^2=9-4`
`AB^2=5`
`AB=sqrt5`
Hence, Base = `sqrt5`
Now, `Cos A=" Base"/ "Hypotenuse"`
Cos A=` sqrt 5/3`
Now, `Sec 4= "Hypotenuse"/"Perpendicluar"`
Therefore,
`"Cosec" A= "Hypotenuse"/"Perpendicular"`
`"Cosec" A=3/2`
Now, `tan A="Perpendicular"/"Base"`
Therefore,
`Sec A=3/sqrt5`
Now, `tan A "Perpendicular"/"Base"`
Therefore,
`tan A= 2/sqrt5`
Now,`Cos A= "Base"/"Perendicluar"`
Therefore,
`Cot A= sqrt 5/2`
APPEARS IN
RELATED QUESTIONS
If cot θ =` 7/8` evaluate `((1+sin θ )(1-sin θ))/((1+cos θ)(1-cos θ))`
In ΔABC, right angled at B. If tan A = `1/sqrt3` , find the value of
- sin A cos C + cos A sin C
- cos A cos C − sin A sin C
If `tan theta = a/b`, find the value of `(cos theta + sin theta)/(cos theta - sin theta)`
If `cos theta = 12/13`, show that `sin theta (1 - tan theta) = 35/156`
Evaluate the Following
4(sin4 60° + cos4 30°) − 3(tan2 60° − tan2 45°) + 5 cos2 45°
Evaluate the Following
(cos 0° + sin 45° + sin 30°)(sin 90° − cos 45° + cos 60°)
Evaluate the Following:
`tan 45^@/(cosec 30^@) + sec 60^@/cot 45^@ - (5 sin 90^@)/(2 cos 0^@)`
If sin 2A = `1/2` tan² 45° where A is an acute angle, then the value of A is ______.
The value of the expression `[(sin^2 22^circ + sin^2 68^circ)/(cos^2 22^circ + cos^2 68^circ) + sin^2 63^circ + cos 63^circ sin 27^circ]` is ______.
If sinθ = `1/sqrt(2)` and `π/2 < θ < π`. Then the value of `(sinθ + cosθ)/tanθ` is ______.
