Advertisements
Advertisements
Questions
If `cos θ = 12/13`, show that `sin θ (1 - tan θ) = 35/156`.
If `cos θ = 12/13`, verify that `sin θ (1 - tan θ) = 35/156`.
Advertisements
Solution
Given: cos θ = `12/13`
To prove: sin θ (1 – tan θ) = `35/156`
Proof: We know, cos θ = `B/H`
where the right-angled triangle’s base is B and its hypotenuse is H. ∠ACB = 8 is achieved by building a right triangle ABC at a right angle to B.
AB is perpendicular, BC = 12 is base, and AC = 13 is hypotenuse.
According to Pythagoras theorem, we have
AC2 = AB2 + BC2
132 = AB2 + 122
169 = AB2 + 144
169 – 144 = AB2
25 = AB2
AB = `sqrt25`
AB = 5
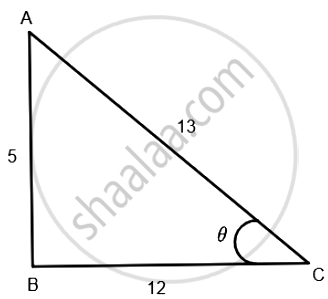
sin θ = `P/H = 5/13`
So, tan θ = `P/H = 5/12`
Put the values in sin θ (1 – tan θ) to find its value,
sin θ (1 – tan θ) = `15/3 (1 - 5/12)`
= `5/13 xx 7/12`
= `35/156`
Hence Proved.
RELATED QUESTIONS
In Given Figure, find tan P – cot R.
If sin A = `3/4`, calculate cos A and tan A.
State whether the following are true or false. Justify your answer.
sec A = `12/5` for some value of angle A.
State whether the following are true or false. Justify your answer.
sin θ = `4/3`, for some angle θ.
In the following, trigonometric ratios are given. Find the values of the other trigonometric ratios.
`cos A = 4/5`
If tan θ = `a/b` prove that `(a sin theta - b cos theta)/(a sin theta + b cos theta) = (a^2 - b^2)/(a^2 + b^2)`
If `sec θ = 13/5`, show that `(2 sin θ - 3 cos θ)/(4 sin θ - 9 cos θ) = 3`.
If `tan theta = 1/sqrt7` `(cosec^2 theta - sec^2 theta)/(cosec^2 theta + sec^2 theta) = 3/4`
if `cot theta = 3/4` prove that `sqrt((sec theta - cosec theta)/(sec theta +cosec theta)) = 1/sqrt7`
Evaluate the following
cos2 30° + cos2 45° + cos2 60° + cos2 90°
Evaluate the Following
cosec3 30° cos 60° tan3 45° sin2 90° sec2 45° cot 30°
Evaluate the Following
(cos 0° + sin 45° + sin 30°)(sin 90° − cos 45° + cos 60°)
Find the value of x in each of the following :
cos x = cos 60º cos 30º + sin 60º sin 30º
If cos (81 + θ)° = sin`("k"/3 - theta)^circ` where θ is an acute angle, then the value of k is ______.
If sin 2A = `1/2` tan² 45° where A is an acute angle, then the value of A is ______.
If x sin (90° – θ) cot (90° – θ) = cos (90° – θ), then x is equal to ______.
If sin θ + sin² θ = 1, then cos² θ + cos4 θ = ______.
5 tan² A – 5 sec² A + 1 is equal to ______.
Find the value of sin 45° + cos 45° + tan 45°.
`sqrt(3)` cos2A + `sqrt(3)` sin2A is equal to ______.
Prove that `tan θ/(1 - cot θ) + cot θ/(1 - tanθ)` = 1 + sec θ cosec θ
If sin θ + cos θ = `sqrt(2)` then tan θ + cot θ = ______.
Find an acute angle θ when `(cos θ - sin θ)/(cos θ + sin θ) = (1 - sqrt(3))/(1 + sqrt(3))`
If f(x) = `3cos(x + (5π)/6) - 5sinx + 2`, then maximum value of f(x) is ______.
If cosec θ = `("p" + "q")/("p" - "q")` (p ≠ q ≠ 0), then `|cot(π/4 + θ/2)|` is equal to ______.
If θ is an acute angle and sin θ = cos θ, find the value of tan2 θ + cot2 θ – 2.
If sin θ – cos θ = 0, then find the value of sin4 θ + cos4 θ.
