Advertisements
Advertisements
Question
Evaluate the following
cos 60° cos 45° - sin 60° ∙ sin 45°
Solution
cos 60° cos 45° - sin 60° ∙ sin 45° …(i)
By trigonometric ratios we know that,
`cos 60^@ = 1/2 cos 45^@ = 1/sqrt2`
`sin 60^@ = sqrt3/2 sin 45^@ = 1/sqrt2`
By substituting above value in (i), we get
`1/2. 1/sqrt2 - sqrt3/2. 1/sqrt2 => (1 - sqrt3)/(2sqrt2)`
APPEARS IN
RELATED QUESTIONS
State whether the following are true or false. Justify your answer.
cos A is the abbreviation used for the cosecant of angle A.
If `tan theta = a/b`, find the value of `(cos theta + sin theta)/(cos theta - sin theta)`
sin (45° + θ) – cos (45° – θ) is equal to ______.
`(sin theta)/(1 + cos theta)` is ______.
If x sin (90° – θ) cot (90° – θ) = cos (90° – θ), then x is equal to ______.
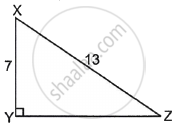
In the given figure, if sin θ = `7/13`, which angle will be θ?
Let tan9° = `(1 - sqrt((sqrt(5)k)/m))k` where k = `sqrt(5) + 1` then m is equal to ______.
If sinθ = `1/sqrt(2)` and `π/2 < θ < π`. Then the value of `(sinθ + cosθ)/tanθ` is ______.
If θ is an acute angle and sin θ = cos θ, find the value of tan2 θ + cot2 θ – 2.
In a right triangle PQR, right angled at Q. If tan P = `sqrt(3)`, then evaluate 2 sin P cos P.