Advertisements
Advertisements
Question
In a right triangle PQR, right angled at Q. If tan P = `sqrt(3)`, then evaluate 2 sin P cos P.
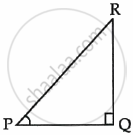
Solution
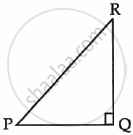
We have,
`\implies` tan P = `sqrt(3)`
`\implies` tan P = `(RQ)/(PQ)`
= `sqrt(3)`
= tan 60°
`\implies` P = 60°
So, 2 sin P cos P = 2 × 60° × cos 60°
= `2 xx sqrt(3)/2 xx 1/2`
= `sqrt(3)/2`
APPEARS IN
RELATED QUESTIONS
In the following, trigonometric ratios are given. Find the values of the other trigonometric ratios.
`cosec theta = sqrt10`
Evaluate the following
`2 sin^2 30^2 - 3 cos^2 45^2 + tan^2 60^@`
Evaluate the following
`sin^2 30° cos^2 45 ° + 4 tan^2 30° + 1/2 sin^2 90° − 2 cos^2 90° + 1/24 cos^2 0°`
sin (45° + θ) – cos (45° – θ) is equal to ______.
If `sqrt2 sin (60° – α) = 1` then α is ______.
If cos A + cos² A = 1, then sin² A + sin4 A is equal to ______.
3 sin² 20° – 2 tan² 45° + 3 sin² 70° is equal to ______.
The value of the expression (sin 80° – cos 80°) is negative.
In ΔABC, ∠ABC = 90° and ∠ACB = θ. Then write the ratios of sin θ and tan θ from the figure.
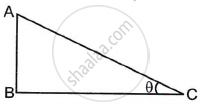
Evaluate 2 sec2 θ + 3 cosec2 θ – 2 sin θ cos θ if θ = 45°.
