Advertisements
Advertisements
प्रश्न
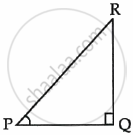
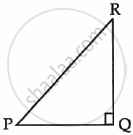
In a right triangle PQR, right angled at Q. If tan P = `sqrt(3)`, then evaluate 2 sin P cos P.
उत्तर
We have,
`\implies` tan P = `sqrt(3)`
`\implies` tan P = `(RQ)/(PQ)`
= `sqrt(3)`
= tan 60°
`\implies` P = 60°
So, 2 sin P cos P = 2 × 60° × cos 60°
= `2 xx sqrt(3)/2 xx 1/2`
= `sqrt(3)/2`
APPEARS IN
संबंधित प्रश्न
In ΔABC, right angled at B. If tan A = `1/sqrt3` , find the value of
- sin A cos C + cos A sin C
- cos A cos C − sin A sin C
State whether the following are true or false. Justify your answer.
sec A = `12/5` for some value of angle A.
If 4 tan θ = 3, evaluate `((4sin theta - cos theta + 1)/(4sin theta + cos theta - 1))`
If 3 cot θ = 2, find the value of `(4sin theta - 3 cos theta)/(2 sin theta + 6cos theta)`.
If `cos theta = 12/13`, show that `sin theta (1 - tan theta) = 35/156`
If Cosec A = 2 find `1/(tan A) + (sin A)/(1 + cos A)`
Evaluate the following
cos2 30° + cos2 45° + cos2 60° + cos2 90°
If sin (A − B) = sin A cos B − cos A sin B and cos (A − B) = cos A cos B + sin A sin B, find the values of sin 15° and cos 15°.
5 tan² A – 5 sec² A + 1 is equal to ______.
Evaluate: 5 cosec2 45° – 3 sin2 90° + 5 cos 0°.
