Advertisements
Advertisements
प्रश्न
If 4 tan θ = 3, evaluate `((4sin theta - cos theta + 1)/(4sin theta + cos theta - 1))`
उत्तर
Given: 4 tan θ = 3 ⇒ tan θ = 3/4
Let us suppose a right angle triangle ABC right angled at B, with one of the acute angle θ. Let the sides be BC = 3kand AB = 4k, where k is a positive number
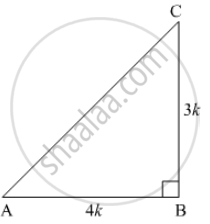
By Pythagoras theorem, we get
`AC^2 = BC^2 + AB^2`
`AC^2 = (3k)^2 + (4k)^2`
`AC^2 = 9k^2 + 16k^2`
`AC = sqrt(25k^2)`
`AC = +- 5k`
Ignoring AC = − 5k , as k is a positive number, we get
AC = 5k
if `tan theta = (BC)/(AB) = 3/4` then `sin theta = (BC)/(AC) = 3/5` and `cos theta = (AB)/(AC) = 4/5`
Putting the values in `((4 sin theta - cos theta + 1)/(4 sin theta + cos theta - 1))` we get
`((4xx3/5 - 4/5 + 1)/(4xx 3/5 + 4/5 -1)) = (((12- 4 + 5)/5)/((12 + 4 - 5)/5)) = 13/11`
APPEARS IN
संबंधित प्रश्न
In Given Figure, find tan P – cot R.

In the following, trigonometric ratios are given. Find the values of the other trigonometric ratios.
`sin theta = 11/5`
In the following, one of the six trigonometric ratios is given. Find the values of the other trigonometric ratios.
`tan alpha = 5/12`
If `cot theta = 1/sqrt3` show that `(1 - cos^2 theta)/(2 - sin^2 theta) = 3/5`
If sin θ = `12/13`, Find `(sin^2 θ - cos^2 θ)/(2sin θ cos θ) × 1/(tan^2 θ)`.
Evaluate the following
sin2 30° + sin2 45° + sin2 60° + sin2 90°
Evaluate the Following
4(sin4 60° + cos4 30°) − 3(tan2 60° − tan2 45°) + 5 cos2 45°
sin (45° + θ) – cos (45° – θ) is equal to ______.
`(1 + tan^2 "A")/(1 + cot^2 "A")` is equal to ______.
Find the value of sin 45° + cos 45° + tan 45°.
