Advertisements
Advertisements
प्रश्न
State whether the following are true or false. Justify your answer.
The value of tan A is always less than 1.
पर्याय
True
False
उत्तर
This statement is False.
Explanation:
Consider a ΔABC, right-angled at B.
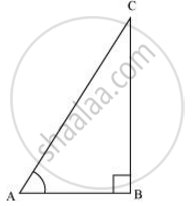
tan A = `("Side opposite to ∠A")/("Side adjacent to ∠A")`
= `12/5`
But `12/5 > 1`
∴ tan A > 1
So, tan A < 1 is not always true.
Hence, the given statement is false.
A tangent of an angle is the ratio of sides other than hypotenuse, which may be equal or unequal to each other.
संबंधित प्रश्न
In ΔABC right angled at B, AB = 24 cm, BC = 7 m. Determine:
sin C, cos C
In ΔABC, right angled at B. If tan A = `1/sqrt3` , find the value of
- sin A cos C + cos A sin C
- cos A cos C − sin A sin C
In the following, one of the six trigonometric ratios is given. Find the values of the other trigonometric ratios.
`cot theta = 12/5`
In the following, one of the six trigonometric ratios is given. Find the values of the other trigonometric ratios.
`cos theta = 12/2`
If 3 tan θ = 4, find the value of `(4cos theta - sin theta)/(2cos theta + sin theta)`
If 3 cot θ = 2, find the value of `(4sin theta - 3 cos theta)/(2 sin theta + 6cos theta)`.
If tan θ = `a/b` prove that `(a sin theta - b cos theta)/(a sin theta + b cos theta) = (a^2 - b^2)/(a^2 + b^2)`
Evaluate the following
tan2 30° + tan2 60° + tan2 45°
Evaluate the Following
4(sin4 60° + cos4 30°) − 3(tan2 60° − tan2 45°) + 5 cos2 45°
Evaluate the following:
(cosec2 45° sec2 30°)(sin2 30° + 4 cot2 45° − sec2 60°)
Evaluate the Following
`cot^2 30^@ - 2 cos^2 60^circ- 3/4 sec^2 45^@ - 4 sec^2 30^@`
If sin 2A = `1/2` tan² 45° where A is an acute angle, then the value of A is ______.
`(sin theta)/(1 + cos theta)` is ______.
The value of cos 0°. cos 1°. cos 2°. cos 3°… cos 89° cos 90° is ______.
If 4 tanθ = 3, then `((4 sintheta - costheta)/(4sintheta + costheta))` is equal to ______.
The value of the expression (sin 80° – cos 80°) is negative.
Prove that `tan θ/(1 - cot θ) + cot θ/(1 - tanθ)` = 1 + sec θ cosec θ
If f(x) = `3cos(x + (5π)/6) - 5sinx + 2`, then maximum value of f(x) is ______.
In a right triangle PQR, right angled at Q. If tan P = `sqrt(3)`, then evaluate 2 sin P cos P.
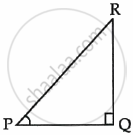
Evaluate: 5 cosec2 45° – 3 sin2 90° + 5 cos 0°.
