Advertisements
Advertisements
प्रश्न
State whether the following are true or false. Justify your answer.
sec A = `12/5` for some value of angle A.
पर्याय
True
False
उत्तर
This statement is True.
Explanation:
sec A = `12/5`
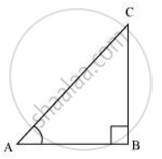
`"Hypotenuse"/"Side adjacent to ∠A" - 12/5`
`("AC")/("AB") = (12/5)`
Let AC be 12k, AB will be 5k, where k is a positive integer.
Applying Pythagoras theorem in ΔABC, we obtain
AC2 = AB2 + BC2
(12k)2 = (5k)2 + BC2
144k2 = 25k2 + BC2
BC2 = 119k2
BC = 10.9k
It can be observed that for given two sides AC = 12k and AB = 5k,
BC should be such that,
AC − AB < BC < AC + AB
12k − 5k < BC < 12k + 5k
7k < BC < 17 k
However, BC = 10.9k
Clearly, such a triangle is possible and hence, such value of sec A is possible.
Hence, the given statement is true.
संबंधित प्रश्न
If sin A = `3/4`, calculate cos A and tan A.
State whether the following are true or false. Justify your answer.
cot A is the product of cot and A.
Prove that `(sin "A" - 2sin^3 "A")/(2cos^3 "A" - cos "A") = tan "A"`
In the following, trigonometric ratios are given. Find the values of the other trigonometric ratios.
`cos A = 4/5`
In the following, one of the six trigonometric ratios is given. Find the values of the other trigonometric ratios.
`tan alpha = 5/12`
If `cos theta = 12/13`, show that `sin theta (1 - tan theta) = 35/156`
If `tan theta = 1/sqrt7` `(cosec^2 theta - sec^2 theta)/(cosec^2 theta + sec^2 theta) = 3/4`
If Cosec A = 2 find `1/(tan A) + (sin A)/(1 + cos A)`
Evaluate the following
sin 45° sin 30° + cos 45° cos 30°
The value of sin² 30° – cos² 30° is ______.
If cos (40° + A) = sin 30°, then value of A is ______.
If cos A + cos² A = 1, then sin² A + sin4 A is equal to ______.
`(sin theta)/(1 + cos theta)` is ______.
5 tan² A – 5 sec² A + 1 is equal to ______.
Prove that sec θ + tan θ = `cos θ/(1 - sin θ)`.
Proof: L.H.S. = sec θ + tan θ
= `1/square + square/square`
= `square/square` ......`(∵ sec θ = 1/square, tan θ = square/square)`
= `((1 + sin θ) square)/(cos θ square)` ......[Multiplying `square` with the numerator and denominator]
= `(1^2 - square)/(cos θ square)`
= `square/(cos θ square)`
= `cos θ/(1 - sin θ)` = R.H.S.
∴ L.H.S. = R.H.S.
∴ sec θ + tan θ = `cos θ/(1 - sin θ)`
Find the value of sin 45° + cos 45° + tan 45°.
Find an acute angle θ when `(cos θ - sin θ)/(cos θ + sin θ) = (1 - sqrt(3))/(1 + sqrt(3))`
Evaluate 2 sec2 θ + 3 cosec2 θ – 2 sin θ cos θ if θ = 45°.
In ΔBC, right angled at C, if tan A = `8/7`, then the value of cot B is ______.