Advertisements
Advertisements
प्रश्न
In ΔABC right angled at B, AB = 24 cm, BC = 7 m. Determine:
sin C, cos C
उत्तर
ΔABC is right angled at B
AB = 24cm, BC = 7cm.
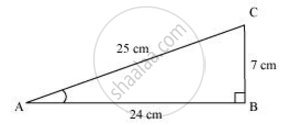
Let ‘x’ be the hypotenuse,
By applying Pythagoras
AC2 = AB2 + BC2
x2 = 242 + 72
x2 = 576 + 49
x2 = 625
x = 25
For Sin C, Cos C
sin C = `("AB")/("AC") = 24/25`
cos C = `("BC")/("AC") = 7/25`
संबंधित प्रश्न
State whether the following are true or false. Justify your answer.
sin θ = `4/3`, for some angle θ.
In the following, trigonometric ratios are given. Find the values of the other trigonometric ratios.
`cos A = 4/5`
In the following, trigonometric ratios are given. Find the values of the other trigonometric ratios.
`sin theta = 11/5`
In the following, trigonometric ratios are given. Find the values of the other trigonometric ratios.
`cos theta = 7/25`
If 3 cot θ = 2, find the value of `(4sin theta - 3 cos theta)/(2 sin theta + 6cos theta)`.
If sin θ = `12/13`, Find `(sin^2 θ - cos^2 θ)/(2sin θ cos θ) × 1/(tan^2 θ)`.
If `tan θ = 20/21` show that `(1 - sin theta + cos theta)/(1 + sin theta + cos theta) = 3/7`
Evaluate the following
sin 45° sin 30° + cos 45° cos 30°
Evaluate the Following
4(sin4 60° + cos4 30°) − 3(tan2 60° − tan2 45°) + 5 cos2 45°
Evaluate the Following:
`tan 45^@/(cosec 30^@) + sec 60^@/cot 45^@ - (5 sin 90^@)/(2 cos 0^@)`
Find the value of x in the following :
`2sin 3x = sqrt3`
sin (45° + θ) – cos (45° – θ) is equal to ______.
If sin θ + sin² θ = 1, then cos² θ + cos4 θ = ______.
The value of the expression `[(sin^2 22^circ + sin^2 68^circ)/(cos^2 22^circ + cos^2 68^circ) + sin^2 63^circ + cos 63^circ sin 27^circ]` is ______.
If 4 tanθ = 3, then `((4 sintheta - costheta)/(4sintheta + costheta))` is equal to ______.
Let tan9° = `(1 - sqrt((sqrt(5)k)/m))k` where k = `sqrt(5) + 1` then m is equal to ______.
If sinθ = `1/sqrt(2)` and `π/2 < θ < π`. Then the value of `(sinθ + cosθ)/tanθ` is ______.
If θ is an acute angle of a right angled triangle, then which of the following equation is not true?
Evaluate: 5 cosec2 45° – 3 sin2 90° + 5 cos 0°.
