Advertisements
Advertisements
рдкреНрд░рд╢реНрди
In the following, trigonometric ratios are given. Find the values of the other trigonometric ratios.
`cos theta = 7/25`
рдЙрддреНрддрд░
We know that `cos theta = "adjacent side"/"hypotence"`
Now consider a right-angled Δle ABC
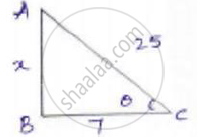
Let x be the opposite side.
By applying Pythagoras theorem
ЁЭР┤ЁЭР╢2 = ЁЭР┤ЁЭР╡2 + ЁЭР╡ЁЭР╢2
(25)2 = ЁЭСе2 + 72
625 - 49 = ЁЭСе2
`576 = sqrt576 = 24`
`sin theta = "opposite side"/"hypotenuse"= 24/25`
`tan theta = "opposite side"/"adjacent side" = 24/7`
`cosec theta = 1/sin theta = (1/3)/5 = 25/24`
`sec theta = 1/cos theta = (1/4)/5 = 25/7`
`cot theta = 1/tan theta = (1/3)/4 = 7/24`
APPEARS IN
рд╕рдВрдмрдВрдзрд┐рдд рдкреНрд░рд╢реНтАНрди
if `sec A = 17/8` verify that `(3 - 4sin^2A)/(4 cos^2 A - 3) = (3 - tan^2 A)/(1 - 3 tan^2 A)`
If `tan θ = 20/21` show that `(1 - sin theta + cos theta)/(1 + sin theta + cos theta) = 3/7`
Evaluate the Following
`(sin 30^@ - sin 90^2 + 2 cos 0^@)/(tan 30^@ tan 60^@)`
If sin 2A = `1/2` tan² 45° where A is an acute angle, then the value of A is ______.
`(sin theta)/(1 + cos theta)` is ______.
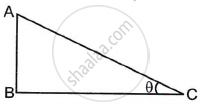
In ΔABC, ∠ABC = 90° and ∠ACB = θ. Then write the ratios of sin θ and tan θ from the figure.
Find the value of sin 45° + cos 45° + tan 45°.
If `θ∈[(5π)/2, 3π]` and 2cosθ + sinθ = 1, then the value of 7cosθ + 6sinθ is ______.
If sinθ = `1/sqrt(2)` and `π/2 < θ < π`. Then the value of `(sinθ + cosθ)/tanθ` is ______.
Evaluate 2 sec2 θ + 3 cosec2 θ – 2 sin θ cos θ if θ = 45°.
