Advertisements
Advertisements
प्रश्न
In triangle ABC, AB = AC = 15 cm and BC = 18 cm. Find:
- cos B
- sin C
- tan2 B - sec2 B + 2
उत्तर

In the isosceles ΔABC, the perpendicular drawn from angle A to the side BC divides the side BC into two equal parts BD = DC = 9 cm
Since ∠ADB = 90°
⇒ AB2 = AD2 + BD2 ...(AB is hypotenuse in ΔABD)
⇒ AD2 = 152 – 92
⇒ AD2 = 144
⇒ AD = `sqrt144`
⇒ AD = 12
(i) cos B = `"base"/"hypotenue" = "BD"/"AB" = (9)/(15) = (3)/(5)`
(ii) sin C = `"perpendicular"/"hypotenuse" = "AD"/"AB" = (12)/(15) = (4)/(5)`
(iii) tan B = `"perpendicular"/"base" = "AD"/"BD" = (12)/(9) = (4)/(3)`
sec B = `"hypotenuse"/"base" = "AB"/"BD" = (15)/(9) = (5)/(3)`
Therefore,
tan2 B – sec2 B + 2
= `(4/3)^2 – (5/3)^2+2`
= `16/9 - 25/9 + 2`
= `16/9 - 25/9 + (2 xx 9)/(1 xx 9)`
= `(16 – 25 + 18)/(9)`
= `9/9`
= 1
APPEARS IN
संबंधित प्रश्न
In Fig below, Find tan P and cot R. Is tan P = cot R?

If A = B = 60°. Verify `tan (A - B) = (tan A - tan B)/(1 + tan tan B)`
If `sin (A – B) = 1/2` and `cos (A + B) = 1/2`, `0^@` < A + `B <= 90^@`, A > B Find A and B.
If A, B, C are the interior angles of a ΔABC, show that `cos[(B+C)/2] = sin A/2`
If Sec 4A = cosec (A – 20°) where 4A is an acute angle, find the value of A.
If tan `theta = a/b`, show that `((a sin theta - b cos theta))/((a sin theta + bcos theta))= ((a^2-b^2))/(a^2+b^2)`
In triangle ABC, AD is perpendicular to BC. sin B = 0.8, BD = 9 cm and tan C = 1.
Find the length of AB, AD, AC, and DC.
In ΔABC, ∠B = 90°. If AB = 12units and BC = 5units, find: sinA
In the given figure, AC = 13cm, BC = 12 cm and ∠B = 90°. Without using tables, find the values of: `("cos A" - "sin A")/("cos A" + "sin A")`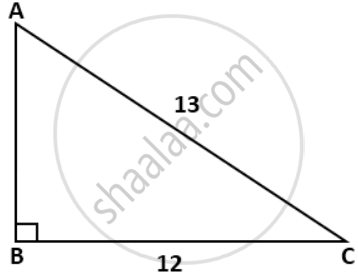
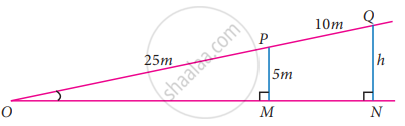
A boy standing at a point O finds his kite flying at a point P with distance OP = 25 m. It is at a height of 5 m from the ground. When the thread is extended by 10 m from P, it reaches a point Q. What will be the height QN of the kite from the ground? (use trigonometric ratios)