Advertisements
Advertisements
प्रश्न
In triangle ABC, AD is perpendicular to BC. sin B = 0.8, BD = 9 cm and tan C = 1.
Find the length of AB, AD, AC, and DC.
उत्तर
Consider the figure below :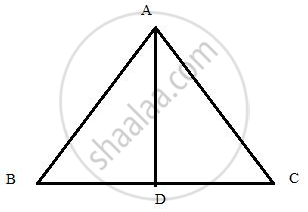
sin B = `(8)/(10) = (4)/(5)`
i.e.`"perpendicular"/"hypotenuse" = "AD"/"AB" = (4)/(5)`
Therefore if length of perpendicular = 4x, length of hypotenuse = 5x
Since
AD2 + BD2 = AB2 ...[ Using Pythagoras Theorem ]
(5x)2 – (4x)2 = BD2
BD2 = 9x2
∴ BD = 3x
Now
BD = 9
3x = 9
x = 3
Therefore
AB = 5x
= 5 x 3
= 15 cm
And
AD= 4x
= 4 x 3
= 12 cm
Again
tan C = `(1)/(1)`
i.e.`"perpendicular"/"base" = "AD"/"DC" = (1)/(1)`
Therefore if length of perpendicular = x, length of base = x
Since
AD2 + DC2 = AC2 ...[ Using Pythagoras Theorem ]
(x)2 + (x)2 = AC2
AC2 = 2x2
∴ AC = `sqrt2x`
Now
AD = 12
x = 12
Therefore
DC = x
= 12 cm
And
AC = `sqrt2`
= `sqrt2` x 12
= 12`sqrt2"cm"`
APPEARS IN
संबंधित प्रश्न
If x = cosec A +cos A and y = cosec A – cos A then prove that `(2/(x+y))^2 + ((x-y)/2)^2` = 1
If A = 300 , verify that:
(i) sin 2A = `(2 tan A)/(1+tan^2A)`
If A = 600 and B = 300, verify that:
(ii) cos (A – B) = cos A cos B + sin A sin B
If A = 600 and B = 300, verify that:
(iii) tan (A-B) = `(tan A-tanB)/(1+tan A tan B)`
If A and B are acute angles such that tan A =`1/3, tan B = 1/2 and tan (A + B) =` show that `A+B = 45^0`
If tan x = `1(1)/(3)`, find the value of : 4 sin2x - 3 cos2x + 2
If sec A = `sqrt2` , find : `(3cot^2 "A"+ 2 sin^2 "A")/ (tan^2 "A" – cos ^2 "A")`.
In ΔABC, ∠A = 90°. If AB = 5 units and AC = 12 units, find: cos C
In the given figure, AD is the median on BC from A. If AD = 8 cm and BC = 12 cm, find the value of cos y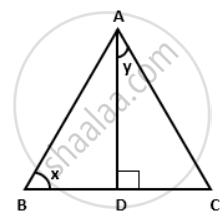
Given that sin α = `1/2` and cos β = `1/2`, then the value of α + β is ______.
