Advertisements
Advertisements
प्रश्न
If x = cosec A +cos A and y = cosec A – cos A then prove that `(2/(x+y))^2 + ((x-y)/2)^2` = 1
उत्तर
LHS = `(2/(x+y))^2 + ((x-y)/2)^2 - 1`
=`[2/((cosec A + cos A)+(cosec A - cos A))]^2 + [((cosecA+cosA)-(cosecA-cosA))/2]^2 - 1`
=`[2/(cosecA + cosA + cosecA-cosA)]^2 + [(cosecA +cosA-cosecA+cosA)/2]^2-1`
=`[2/(2cosecA)]^2 + [(2 cosA)/2]^2-1`
=`[1/(cosecA)]^2 + [cosA]^2-1`
=`[sinA]^2 + [cosA]^2-1`
=`sin^2 A + cos^2 A-1`
=1-1
=0
=RHS
APPEARS IN
संबंधित प्रश्न
In a ΔABC, right angled at A, if tan C = `sqrt3` , find the value of sin B cos C + cos B sin C.
In right angled triangle ΔABC at B, ∠A = ∠C. Find the values of Sin A cos C + Cos A Sin C
If sec `theta = 17/8 ` verify that `((3-4sin^2theta)/(4 cos^2theta -3))=((3-tan^2theta)/(1-tan^2theta))`
If ∠A and ∠B are acute angles such that sin A = Sin B prove that ∠A = ∠B.
Evaluate:
sin600 cos300 + cos600 sin300
If A = 300 , verify that:
(iii) tan 2A = `(2tanA)/(1-tan^2A)`
Using the formula, cos A = `sqrt((1+cos2A)/2) ,`find the value of cos 300, it being given that cos 600 = `1/2`.
In triangle ABC, AB = AC = 15 cm and BC = 18 cm. Find:
- cos B
- sin C
- tan2 B - sec2 B + 2
In the given figure, AC = 13cm, BC = 12 cm and ∠B = 90°. Without using tables, find the values of: sin A cos A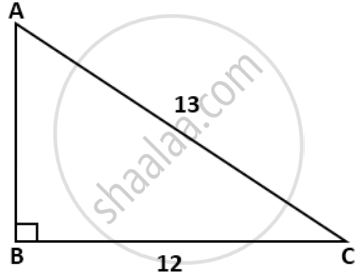
From the given figure, find the values of cosec C