Advertisements
Advertisements
प्रश्न
Evaluate:
sin600 cos300 + cos600 sin300
उत्तर
On substituting the values of various T-ratios, we get:
sin600 cos300 + cos600 sin300
=`(sqrt(3)/2 xxsqrt(3)/2 + 1/2 xx1/2 ) = (3/4 + 1/4 )=4/4 =1`
APPEARS IN
संबंधित प्रश्न
If 3cos θ – 4sin = 2cos θ + sin θ Find tan θ.
If cosec θ = `sqrt(10)` find all the values of all T-ratios of θ
If cosec θ= 2 show that `(cot θ +sin θ /(1+cos θ )) =2`
If sec θ = `5/4 ` show that `((sin θ - 2 cos θ))/(( tan θ - cot θ)) = 12/7`
If cot θ = `3/4` , show that `sqrt("sec θ - cosecθ"/"secθ + cosecθ" ) = 1/ sqrt(7)`
Evaluate:
`(sin30°)/(cos 45°)+(cot45°)/(sec60° )- (sin60°)/(tan45°)+(cos30°)/(sin90°)`
Verify each of the following:
(iii) `2 sin 30^0 cos 30^0`
Prove that
sin (50° + θ ) − cos (40° − θ) + tan 1° tan 10° tan 80° tan 89° = 1.
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
sinB = `sqrt(3)/(2)`
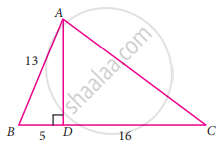
From the given figure, find the values of sec B