Advertisements
Advertisements
प्रश्न
If sec θ = `5/4 ` show that `((sin θ - 2 cos θ))/(( tan θ - cot θ)) = 12/7`
उत्तर
We have ,
sec θ = `5/4`
`⇒ 1/(cos θ) = 5/4`
`⇒ cos θ = 4/5`
Also,
`sin^2 θ = 1-cos^2 θ`
`= 1-(4/5)^2`
`= 1-16/25`
=`9/25`
`⇒ sin θ = 3/5`
Now ,
LHS = `((sin θ -2 cos θ))/((tan θ - cot θ))`
= `((sin θ - 2 cos θ))/(((sin θ cos θ)/(cos θ sin θ))`
=` ((sin θ - 2 - cos θ))/(((sin^2 θ- cos^2 θ)/(sin θ cosθ)))`
`(sinθ cosθ (sinθ-2cosθ))/((sin^2θ-cos^2 θ))`
`=(3/5xx4/5(3/5-2xx4/5))/((3/5)^2-(4/5)^2`
=`(12/25(3/5-8/5))/((9/25-16/25))`
`= (12/25xx((-5)/5))/((-7/25))`
=`12/7`
= RHS
APPEARS IN
संबंधित प्रश्न
if `sec theta = 5/4` find the value of `(sin theta - 2 cos theta)/(tan theta - cot theta)`
If sin θ ,` sqrt (3)/2` find the value of all T- ratios of θ .
Show that:
(ii) `(cos30^0+sin 60^0)/(1+sin30^0+cos60^0)=cos 30^0`
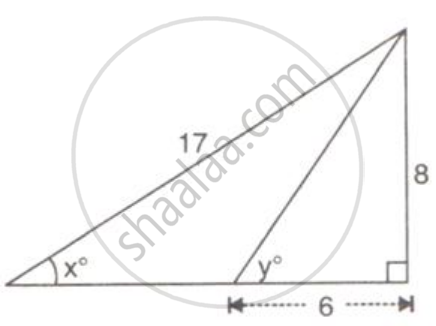
Use the given figure to find :
(i) sin xo
(ii) cos yo
(iii) 3 tan xo - 2 sin yo + 4 cos yo.
If 2 sin x = `sqrt3` , evaluate.
(i) 4 sin3 x - 3 sin x.
(ii) 3 cos x - 4 cos3 x.
If 5 cos θ = 3, evaluate : `(co secθ – cot θ)/(co secθ + cot θ)`
In ΔABC, ∠B = 90°. If AB = 12units and BC = 5units, find: sinA
In the given figure, PQR is a triangle, in which QS ⊥ PR, QS = 3 cm, PS = 4 cm and QR = 12 cm, find the value of: cot2P - cosec2P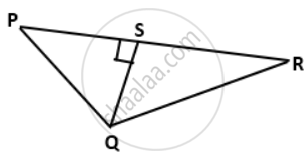
If cos A = `(2x)/(1 + x^2)`, then find the values of sin A and tan A in terms of x
If sin θ = `"a"/sqrt("a"^2 + "b"^2)`, then show that b sin θ = a cos θ
