Advertisements
Advertisements
Question
If sec θ = `5/4 ` show that `((sin θ - 2 cos θ))/(( tan θ - cot θ)) = 12/7`
Solution
We have ,
sec θ = `5/4`
`⇒ 1/(cos θ) = 5/4`
`⇒ cos θ = 4/5`
Also,
`sin^2 θ = 1-cos^2 θ`
`= 1-(4/5)^2`
`= 1-16/25`
=`9/25`
`⇒ sin θ = 3/5`
Now ,
LHS = `((sin θ -2 cos θ))/((tan θ - cot θ))`
= `((sin θ - 2 cos θ))/(((sin θ cos θ)/(cos θ sin θ))`
=` ((sin θ - 2 - cos θ))/(((sin^2 θ- cos^2 θ)/(sin θ cosθ)))`
`(sinθ cosθ (sinθ-2cosθ))/((sin^2θ-cos^2 θ))`
`=(3/5xx4/5(3/5-2xx4/5))/((3/5)^2-(4/5)^2`
=`(12/25(3/5-8/5))/((9/25-16/25))`
`= (12/25xx((-5)/5))/((-7/25))`
=`12/7`
= RHS
APPEARS IN
RELATED QUESTIONS
If 3cos θ – 4sin = 2cos θ + sin θ Find tan θ.
f θ = 30°, verify that cos 3θ = 4 cos3 θ − 3 cos θ
If sec `theta = 17/8 ` verify that `((3-4sin^2theta)/(4 cos^2theta -3))=((3-tan^2theta)/(1-tan^2theta))`
If A = 600 and B = 300, verify that:
(i) sin (A + B) = sin A cos B + cos A sin B
Using the formula, sin A = `sqrt((1-cos 2A)/2) ` find the value of sin 300, it being given that cos 600 = `1/2`
From the following figure, find the values of
(i) cos A
(ii) cosec A
(iii) tan2A - sec2A
(iv) sin C
(v) sec C
(vi) cot2 C - ` 1 / sin^2 "c"`
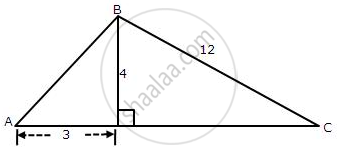
In triangle ABC, AB = AC = 15 cm and BC = 18 cm, find cos ∠ABC.
In a right-angled triangle PQR, ∠PQR = 90°, QS ⊥ PR and tan R =`(5)/(12)`, find the value of sin ∠PQS
From the given figure, find the values of tan C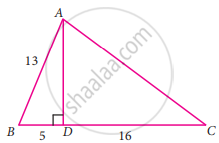
If sin θ = `"a"/sqrt("a"^2 + "b"^2)`, then show that b sin θ = a cos θ
