Advertisements
Advertisements
Question
If tan θ = `20/21` show that `((1-sin θ + cos θ))/((1+ sin θ +cos θ)) = 3/7`
Solution
Let us consider a right ΔABC right angled at B and ∠𝐶 = 𝜃
Now, we know that tan 𝜃 = `(AB)/(BC) = 20/21`

So, if AB = 20k, then BC = 21k, where k is a positive number.
Using Pythagoras theorem, we get:
`AC^2 = AB^2 + BC^2`
`⟹ AC^2 = (20K)^2 + (21K)^2`
`⟹ AC^2 = 841K^2`
⟹ 𝐴𝐶 = 29𝑘
Now. Sin 𝜃 = `(AB)/(AC) = 20/29 and cos θ =(BC)/(AC)=21/29`
Substituting these values in the give expression, we get:
LHS = `(1- sin θ + cos θ )/(1+ sin θ + cos θ )`
=` (1-20/29+21/29)/(1+20/29+21/29)`
=` ((29-20+21)/29)/((29+20+21)/29) = 30/70 = 3/7 = `𝑅𝐻𝑆
∴ LHS = RHS
Hence proved.
APPEARS IN
RELATED QUESTIONS
If sin θ = ` (a^2 - b^2)/(a^2+b^2)`find all the values of all T-ratios of θ .
If tan `theta = a/b`, show that `((a sin theta - b cos theta))/((a sin theta + bcos theta))= ((a^2-b^2))/(a^2+b^2)`
If sin (A + B) = 1 and cos (A – B) = 1, 00 ≤ (A + B) ≤ 900 and A > B, then find A and B.
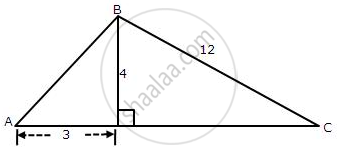
From the following figure, find the values of
(i) cos A
(ii) cosec A
(iii) tan2A - sec2A
(iv) sin C
(v) sec C
(vi) cot2 C - ` 1 / sin^2 "c"`
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
cotA = `(1)/(11)`
In ΔABC, ∠A = 90°. If AB = 5 units and AC = 12 units, find: sinB
In ΔABC, ∠B = 90°. If AB = 12units and BC = 5units, find: cot C
If sinA = `(3)/(5)`, find cosA and tanA.
If 2 cos θ = `sqrt(3)`, then find all the trigonometric ratios of angle θ
Given that sin α = `1/2` and cos β = `1/2`, then the value of α + β is ______.
