Advertisements
Advertisements
Question
If sin θ = ` (a^2 - b^2)/(a^2+b^2)`find all the values of all T-ratios of θ .
Solution
We have sin θ = `(a^2 - b^2)/(a^2 + b^2)`
As,
`Cos^2 θ = 1 - sin^2 θ`
`= 1- ((a^2 -b^2)/(a^2 + b^2))^2`
`= 1/1 - ((a^2 - b^2)/(a^2 + b^2))^2`
`= ((a^2 + b^2)^2 -( a^2 - b^2)^2)/(a^2 + b^2)^2`
`= ([(a^2 +b^2)-(a^2-b^2)][(a^2+b^2)+(a^2-b^2)])/((a^2+b^2)^2)`
`= ([(a^2 + b^2-a^2 +b^2][a^2+b^2+a^2-b^2)])/((a^2+b^2)^2)`
`= ([2b^2][2a^2])/((a^2+b^2)^2)`
`= cos^2 θ = (4a^2b^2)/((a^2+b^2)^2)`
`= cosθ= sqrt((4a^2b^2)/(a^2+b^2)^2)`
`⟹ cos θ =(2ab)/((a^2+b^2))`
Also,
tan θ = `sinθ/cosθ`
`= (((a^2-b^2)/(a^2+b^2)))/(((2ab)/(a^2 +b^2))`
`=(a^2-b^2)/(2ab)`
Now ,
cosec θ =` 1/sinθ`
=`1/(((a^2-b^2)/(a^2-b^2)))`
`= (a^2 + b^2)/(2ab)`
Also,
sec θ`= 1/(cosθ)`
= `1/(((2ab)/(a^2+b^2)))`
= `(a^2+b^2)/(2ab)`
And,
cot θ = `1/( tan θ)`
`= 1/(((a^2-b^2)/(2ab)))`
`= (2ab)/(a^2-b^2)`
APPEARS IN
RELATED QUESTIONS
If sin θ = cos (θ – 45°), where θ – 45° are acute angles, find the degree measure of θ
In a ΔABC , ∠B = 90° , AB = 12 cm and BC = 5 cm Find
(i) cos A (ii) cosec A (iii) cos C (iv) cosec C
If sin ∝ = `1/2` prove that (3cos∝ - `4cos^2` ∝)=0
Evaluate:
`(sin30°)/(cos 45°)+(cot45°)/(sec60° )- (sin60°)/(tan45°)+(cos30°)/(sin90°)`
If A = 300 , verify that:
(ii) cos 2A = `(1- tan^2A)/(1+tan^2A)`
Using the formula, tan 2A =`(2 tan A )/(1- tan^2 A)` find the value of tan 600, it being given that tan 300 = `1/sqrt(3)`.
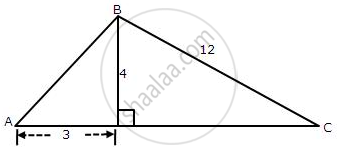
From the following figure, find the values of
(i) cos A
(ii) cosec A
(iii) tan2A - sec2A
(iv) sin C
(v) sec C
(vi) cot2 C - ` 1 / sin^2 "c"`
In rhombus ABCD, diagonals AC and BD intersect each other at point O.
If cosine of angle CAB is 0.6 and OB = 8 cm, find the lengths of the side and the diagonals of the rhombus.
If 5 cos = 6 sin ; evaluate:
(i) tan θ
(ii) `(12 sin θ – 3 cos θ)/(12 sin θ + 3 cos θ)`
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
sinA = `(12)/(13)`
