Advertisements
Advertisements
Question
Using the formula, tan 2A =`(2 tan A )/(1- tan^2 A)` find the value of tan 600, it being given that tan 300 = `1/sqrt(3)`.
Solution
A = 300
⇒ 2A = 2 × 300 = 600
By substituting the value of the given T-ratio, we get:
tan 2A = `(2 tan A )/(1- tan^2 A)`
`⇒ tan 60^0 = (2 tan 30^0)/(1- tan^2 30^0) = (2xx (1/sqrt(3)))/(1-(1/sqrt(3))^2 ` =` ((2/sqrt(3)))/(1-1/3) = ((2/sqrt(3)))/(2/3) = (2/sqrt(3))= 3/2 = sqrt(3) `
∴tan` 60^0 = sqrt(3)`.
APPEARS IN
RELATED QUESTIONS
In Fig below, Find tan P and cot R. Is tan P = cot R?

if `sec theta = 5/4` find the value of `(sin theta - 2 cos theta)/(tan theta - cot theta)`
In a ΔABC , ∠B = 90° , AB = 12 cm and BC = 5 cm Find
(i) cos A (ii) cosec A (iii) cos C (iv) cosec C
Verify each of the following:
(ii)`cos 60^0 cos 30^0+ sin 60^0 sin30^0`
Verify each of the following:
(iii) `2 sin 30^0 cos 30^0`
Given : sin A = `(3)/(5)` , find : (i) tan A (ii) cos A
Given: sin θ = `p/q`.
Find cos θ + sin θ in terms of p and q.
In the figure given below, ABC is an isosceles triangle with BC = 8 cm and AB = AC = 5 cm. Find:
(i) sin B
(ii) tan C
(iii) sin2 B + cos2B
(iv) tan C - cot B
In the given figure, PQR is a triangle, in which QS ⊥ PR, QS = 3 cm, PS = 4 cm and QR = 12 cm, find the value of: cot2P - cosec2P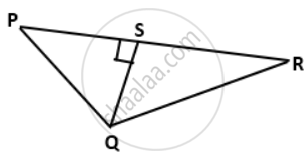
If cos θ : sin θ = 1 : 2, then find the value of `(8costheta - 2sintheta)/(4costheta + 2sintheta`
