Advertisements
Advertisements
Question
In Fig below, Find tan P and cot R. Is tan P = cot R?
Solution
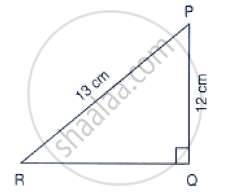
Let x be the adjacent side.
By Pythagoras theorem
๐๐ 2 = ๐๐2 + ๐ ๐2
169 = ๐ฅ2 + 144
๐ฅ2 = 25
๐ฅ = 5
At LP, opposite side = 5
Adjacent side = 12
Hypotenuse = 13
`tan P = (1/12)/5 => 5/12`
At LR, opposite side = 12
Adjacent side = 5
Hypotenuse = 13
`cot R = 1/tan R = 1/(12/5) = 5/12`
`[โต Tan R = "๐๐๐๐๐ ๐๐ก๐ ๐ ๐๐๐"/"๐๐๐๐๐๐๐๐ก ๐ ๐๐๐"]`
โต tan P = cot R
APPEARS IN
RELATED QUESTIONS
If sin θ = ` (a^2 - b^2)/(a^2+b^2)`find all the values of all T-ratios of θ .
If 3 cot θ 4 , show that`((1-tan^2theta))/((1+tan^2theta)) = (cos^2theta - sin^2theta)`
If A = 450 , verify that:
(ii) cos 2A = 2 cos2 A – 1 = 1 – 2 sin2 A
From the following figure, find the values of
(i) cos A
(ii) cosec A
(iii) tan2A - sec2A
(iv) sin C
(v) sec C
(vi) cot2 C - ` 1 / sin^2 "c"`
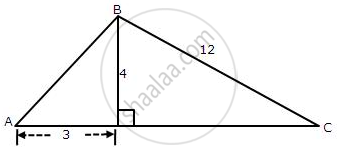
In the diagram, given below, triangle ABC is right-angled at B and BD is perpendicular to AC.
Find:
(i) cos ∠DBC
(ii) cot ∠DBA
In triangle ABC, ∠B = 90° and tan A = 0.75. If AC = 30 cm, find the lengths of AB and BC.
In rectangle ABCD, diagonal BD = 26 cm and cotangent of angle ABD = 1.5. Find the area and the perimeter of the rectangle ABCD.
If sin A = `(7)/(25)`, find the value of : `(2"tanA")/"cot A - sin A"`
From the given figure, find the values of cot B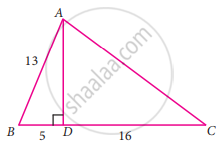
If cos A = `3/5`, then find the value of `(sin"A" - cos"A")/(2tan"A")`
