Advertisements
Advertisements
Question
In triangle ABC, ∠B = 90° and tan A = 0.75. If AC = 30 cm, find the lengths of AB and BC.
Solution
Consider the figure :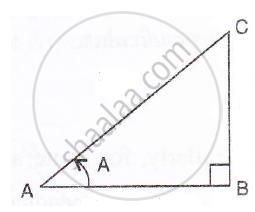
tan A = `(75)/(100) = (3)/(4)`
i.e.`"perpendicular"/"base" = "BC"/"AB" = (3)/(4)`
Therefore if length of base = 4x, length of perpendicular = 3x
Since
BC2 + AB2 = AC2 ...[ Using Pythagoras Theorem ]
(3x)2 + (4x)2 = AC2
AC2 = 9x2 + 16x2 = 25x2
∴ Ac = 5x
Now
Ac = 30
5x = 30
x = 6
Therefore
AB = 4x
= 4 x 6
= 24 cm
And
Bc = 3x
= 3 x 6
= 18 cm
APPEARS IN
RELATED QUESTIONS
If 3 cot A = 4, Check whether `((1-tan^2 A)/(1+tan^2 A)) = cos^2 "A" - sin^2 "A"` or not.
if `sin theta = 3/5 " evaluate " (cos theta - 1/(tan theta))/(2 cot theta)`
If A = 30° B = 60° verify Sin (A + B) = Sin A Cos B + cos A sin B
If cos 2θ = sin 4θ where 2θ, 4θ are acute angles, find the value of θ.
If sin 3θ = cos (θ – 6°) where 3θ and θ − 6° are acute angles, find the value of θ.
If sec 2A = cosec (A – 42°) where 2A is an acute angle. Find the value of A.
If tan θ = `20/21` show that `((1-sin θ + cos θ))/((1+ sin θ +cos θ)) = 3/7`
If cosec θ = `sqrt5`, find the value of:
- 2 - sin2 θ - cos2 θ
- 2 + `1/sin^2"θ" – cos^2"θ"/sin^2"θ"`
In rectangle ABCD, diagonal BD = 26 cm and cotangent of angle ABD = 1.5. Find the area and the perimeter of the rectangle ABCD.
In ΔABC, ∠B = 90°. If AB = 12units and BC = 5units, find: cos C
