Advertisements
Advertisements
Question
if `sin theta = 3/5 " evaluate " (cos theta - 1/(tan theta))/(2 cot theta)`
Solution
We have
`sin theta = 3/5`
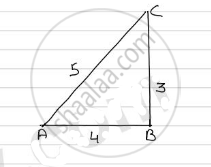
In Δ ABC
`AC^2 = AB^2 + BC^2`
`=> (5)^2 = (3)^2 + (BC)^2`
`=> 25 = 9 + (BC)^2`
`=> (BC)^2 = 25 - 9`
=> (BC)^2 = 16
=> BC = 4
`:. cos theta = 4/5 and cot theta = 4/3`
Now `(cos theta - 1/(tan theta))/(2 cot theta) = ((4/5) - (4/3))/(2 xx 4/3)`
`= ((12 - 20)/15)/(8/3)`
`= (-8)/15 xx 3/8`
`= (-1)/5`
APPEARS IN
RELATED QUESTIONS
f θ = 30°, verify that cos 3θ = 4 cos3 θ − 3 cos θ
If sec 2A = cosec (A – 42°) where 2A is an acute angle. Find the value of A.
If ∠A and ∠B are acute angles such that tan A= Tan B then prove that ∠A = ∠B
cos 40° = sin ______°
From the following figure, find:
(i) y
(ii) sin x°
(iii) (sec x° - tan x°) (sec x° + tan x°)

In triangle ABC; ∠ABC = 90°, ∠CAB = x°, tan x° = `(3)/(4)` and BC = 15 cm. Find the measures of AB and AC.
If sin A = `(sqrt3)/(2)` and cos B = `(sqrt3)/(2)` , find the value of : `(tan"A" – tan"B")/(1+tan"A" tan"B")`
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
sinB = `sqrt(3)/(2)`
In ΔABC, ∠B = 90°. If AB = 12units and BC = 5units, find: sinA
In the given figure, PQR is a triangle, in which QS ⊥ PR, QS = 3 cm, PS = 4 cm and QR = 12 cm, find the value of: 4sin2R - `(1)/("tan"^2"P")`