Advertisements
Advertisements
Question
If sin A = `(sqrt3)/(2)` and cos B = `(sqrt3)/(2)` , find the value of : `(tan"A" – tan"B")/(1+tan"A" tan"B")`
Solution
Consider the diagram below :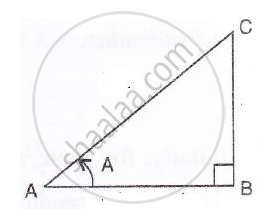 'in A = `(sqrt3)/(2)`
'in A = `(sqrt3)/(2)`
i.e.`"perpendicular"/"hypotenuse" = (sqrt3)/(2) ⇒"BC"/"AC" = (sqrt3)/(2)`
Therefore if length of BC = `sqrt3x`, length of AC = 2x
Since
AB2 + BC2 = AC2 ...[ Using Pythagoras Therorm]
`(sqrt3x)^2 + AB^2 = (2x)^2`
AB2 = x2
∴ AB = x (base)
Consider the diagram below :
cos B = `(sqrt3)/(2)`
i.e.`"base"/"perpendicular" = (sqrt3)/(2) ⇒ "AB"/"BC" = (sqrt3)/(2)`
Therefore if length of AB = `sqrt3x` , length of BC = 2x
Since
AB2 + AC2 = BC2 ...[ Using Pythagoras Theorem ]
AC2 + `(sqrt3x)^2 = (2x)^2`
AC2 = x2
∴ AC = x(perpendicular)
Now
tan A = `"perpendicular"/"base" = (sqrt3x)/(x) = sqrt3`
tan B = `"perpendicular"/"base" = (x)/(sqrt3x) = 1/(sqrt3)`
Therefore
`(tan A – tan B)/(1 + tan A tan B) = (sqrt3 - 1/(sqrt3))/(1+sqrt3 1/(sqrt3)`
= `((2)/(sqrt3))/(2)`
= `(1)/(sqrt3)`
APPEARS IN
RELATED QUESTIONS
If 8 tan A = 15, find sin A – cos A.
Find acute angles A & B, if sin (A + 2B) = `sqrt3/2 cos(A + 4B) = 0, A > B`
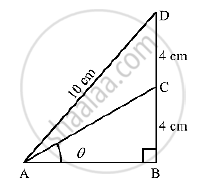
In the adjoining figure, `∠B = 90° , ∠BAC = theta° , BC = CD = 4cm and AD = 10 cm`. find (i) sin theta and (ii) `costheta`
If a right ΔABC , right-angled at B, if tan A=1 then verify that 2sin A . cos A = 1
Using the formula, cos A = `sqrt((1+cos2A)/2) ,`find the value of cos 300, it being given that cos 600 = `1/2`.
Given: cos A = 0.6; find all other trigonometrical ratios for angle A.
In a right-angled triangle, it is given that A is an acute angle and tan A = `(5) /(12)`.
find the value of :
(i) cos A
(ii) sin A
(iii) ` (cosA+sinA)/(cosA– sin A)`
If tan = 0.75, find the other trigonometric ratios for A.
In the given figure, AC = 13cm, BC = 12 cm and ∠B = 90°. Without using tables, find the values of: sin A cos A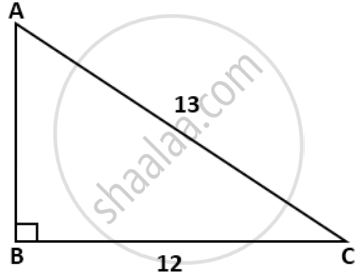
From the given figure, find the values of sin B