Advertisements
Advertisements
Question
If 2 sin x = `sqrt3` , evaluate.
(i) 4 sin3 x - 3 sin x.
(ii) 3 cos x - 4 cos3 x.
Solution
2 sin x = `sqrt3`
sin x = `sqrt3 /(2)`
i.e.`"perpendicular"/"base" = "BC"/"AC" = sqrt3/(2)`
Therefore if length of perpendicular = `sqrt3x` , length of = 2x
Since
AB2 + BC2 = AC2 ...[ Using Pythagoras Theorem]
(2x)2 – (`sqrt3x`)2 = AB2
AB2 = x2
∴ AB = x
Now, cos x = `"AB"/"AC" = (1)/(2)`
(i) 4 sin3 x – 3sin x
= `4 (sqrt3/2)^3 – 3(sqrt3/2)`
= `(3sqrt3)/2 – (3sqrt3)/2`
= 0
(ii) 3 cos x – 4 cos3 x
= `3 * (1)/(2) – 4 * (1/2)^3`
= `3 * 1/2 - 4 * 1/8`
= `3 * 1/2 - cancel4^1 * 1/cancel8_2`
= `3/2 – 1/2`
= 1
APPEARS IN
RELATED QUESTIONS
If A = B = 60°, verify that cos (A − B) = cos A cos B + sin A sin B
If cos θ=0.6 show that (5sin θ -3tan θ) = 0
In the figure of ΔPQR , ∠P = θ° and ∠R =∅° find
(i) `sqrt(X +1) cot ∅`
(ii)`sqrt( x^3 + x ^2) tantheta`
(iii) cos θ

In ΔABC, ∠A = 90°. If AB = 5 units and AC = 12 units, find: tan B.
In ΔABC, ∠B = 90°. If AB = 12units and BC = 5units, find: cot C
From the given figure, find the values of cosec C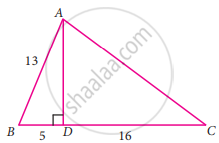
If sin θ = `"a"/sqrt("a"^2 + "b"^2)`, then show that b sin θ = a cos θ
If 3 cot A = 2, then find the value of `(4sin"A" - 3cos"A")/(2sin"A" + 3cos"A")`
A boy standing at a point O finds his kite flying at a point P with distance OP = 25 m. It is at a height of 5 m from the ground. When the thread is extended by 10 m from P, it reaches a point Q. What will be the height QN of the kite from the ground? (use trigonometric ratios)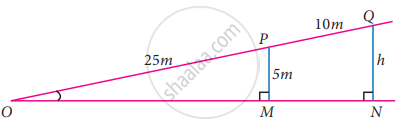
Statement A (Assertion): For 0 < θ ≤ 90°, cosec θ – cot θ and cosec θ + cot θ are reciprocal of each other.
Statement R (Reason): cosec2 θ – cot2 θ = 1
