Advertisements
Advertisements
Question
In the figure of ΔPQR , ∠P = θ° and ∠R =∅° find
(i) `sqrt(X +1) cot ∅`
(ii)`sqrt( x^3 + x ^2) tantheta`
(iii) cos θ

Solution
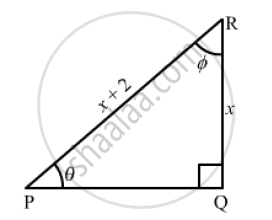
In Δ𝑃𝑄𝑅, ∠𝑄 = 900,
Using Pythagoras theorem, we get
𝑃𝑄 = `sqrt(PR^2 − QR^2)`
= `sqrt ((x + 2)^2 − x^2)`
= `sqrt(x^2 + 4x + 4 − x^2)`
= `sqrt(4 (x+ 1))`
= `2sqrt(x + 1)`
Now,
(i) `(sqrt(x+1) cot theta`
=`(sqrt(x+1))xx(QR)/(PQ)`
=`(sqrt(x+1))xx x/(2 sqrt(x+1))`
=`x/2`
(ii) `(sqrt(x^3+x^2)) tan theta`
= `(sqrt(x^2(x+1)))xx(QR)/(PQ)`
`=x sqrt((x+1))xx x/(2sqrt(x+1)`
= `x^2/2`
(iii) cos θ
=`(PQ)/(PR) theta=(2sqrt(x+1))/(x+2)`
APPEARS IN
RELATED QUESTIONS
Given 15 cot A = 8. Find sin A and sec A.
if `cos theta = 5/13` find the value of `(sin^2 theta - cos^2 theta)/(2 sin theta cos theta) = 3/5`
If A, B, C are the interior angles of a ΔABC, show that `cos[(B+C)/2] = sin A/2`
If tan θ = `4/3`, show that `(sintheta + cos theta )=7/5`
If sin (A – B) = `1/2` and cos (A + B) = `1/2, 0^0 ≤ (A + B) ≤ 90^0` and A > B, then find A and B.
If sec A = `sqrt2`, find the value of :
`(3cos^2"A"+5tan^2"A")/(4tan^4"A"–sin^2"A")`
In triangle ABC, AB = AC = 15 cm and BC = 18 cm, find cos ∠ABC.
If 5 cos = 6 sin ; evaluate:
(i) tan θ
(ii) `(12 sin θ – 3 cos θ)/(12 sin θ + 3 cos θ)`
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
tan C = `(5)/(12)`
In ΔABC, ∠B = 90°. If AB = 12units and BC = 5units, find: cos C
