Advertisements
Advertisements
Question
If tan θ = `4/3`, show that `(sintheta + cos theta )=7/5`
Solution
Let us consider a right ΔABC, right angled at B and ∠𝐶 = 𝜃
Now, we know that tan 𝜃 = `(AB)/(BC) = 4/3`
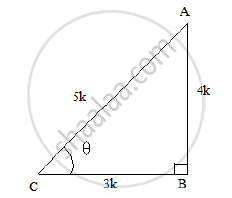
So, if BC = 3k, then AB = 4k, where k is a positive number.
Using Pythagoras theorem, we have:
`AC^2 = AB^2 + BC^2 = (4K)^2 + (3K)^2`
`⟹ AC^2 = 16K^2 + 9K^2 = 25K^2`
⟹ AC = 5k
Finding out the values of sin 𝜃 𝑎𝑛𝑑 cos 𝜃 𝑢𝑠𝑖𝑛𝑔 𝑡ℎ𝑒𝑖𝑟 𝑑𝑒𝑓𝑖𝑛𝑖𝑡𝑖𝑜𝑛𝑠, 𝑤𝑒 ℎ𝑎𝑣𝑒:
Sin 𝜃 = `(AB)/(AC) = (4K)/(5K)=4/5`
`Cos theta= (BC)/(AC) =(3K)/(5K)=3/5`
Substituting these values in the given expression, we get:
`(sin theta + cos theta )=(4/5 +3/5)=(7/5) = RHS`
i.e., LHS = RHS
Hence proved.
APPEARS IN
RELATED QUESTIONS
if `cos theta = 5/13` find the value of `(sin^2 theta - cos^2 theta)/(2 sin theta cos theta) = 3/5`
If tan θ = `1/sqrt(7) `show that ` (cosec ^2 θ - sec^2 θ)/(cosec^2 θ + sec^2 θ ) = 3/4`
If sin θ = `a/b`, show that `(sectheta + tan theta) = sqrt((b+a)/(b-a))`
In a ΔABC , ∠B = 90° , AB = 12 cm and BC = 5 cm Find
(i) cos A (ii) cosec A (iii) cos C (iv) cosec C
If A = 600 and B = 300, verify that:
cos (A + B) = cos A cos B - sin A sin B
sin20° = cos ______°
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
tanB = `(8)/(15)`
From the given figure, find the values of cot B
From the given figure, prove that θ + ∅ = 90°. Also prove that there are two other right angled triangles. Find sin α, cos β and tan ∅
Assertion (A): For 0 < 0 ≤ 90°, cosec θ – cot θ and cosec θ + cot θ are reciprocal of each other.
Reason (R): cot2 θ – cosec2 θ = 1.
