Advertisements
Advertisements
Question
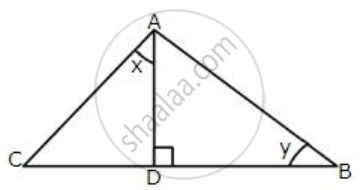
From the given figure, prove that θ + ∅ = 90°. Also prove that there are two other right angled triangles. Find sin α, cos β and tan ∅
Solution
In the ΔABC,
AB = 9 + 16 = 25
AC = 15, BC = 20
AB2 = 252
= 625 ...(1)
AC2 + BC2 = 152 + 202
= 225 + 400
= 625 ...(2)
From (1) and (2) we get
AB2 = AC2 + BC2
ABC is a right angle triangle at C ...(Pythagoras theorem)
∴ ∠C = 90°
θ + ∅ = 90°
Also ADC is a right angle triangle ∠ADC = 90° ...(Given)
BDC is also a right angle triangle ∠BDC = 90° ...(since ADB is a straight line sum of the two angle is 180°)
From the given diagram
sin α = `"DC"/"AC" = 12/15 = 4/5`
cos β = `"BD"/"BC" = 16/20 = 4/5`
tan Φ = `"BD"/"CD" = 16/12 = 4/3`
APPEARS IN
RELATED QUESTIONS
If ∠A and ∠P are acute angles such that tan A = tan P, then show that ∠A = ∠P.
If sin θ = cos (θ – 45°), where θ – 45° are acute angles, find the degree measure of θ
Evaluate:
cos450 cos300 + sin450 sin300
If sin (A – B) = `1/2` and cos (A + B) = `1/2, 0^0 ≤ (A + B) ≤ 90^0` and A > B, then find A and B.
`(cos 28°)/(sin 62°)` = ?
From the following figure, find the values of :
(i) sin A
(ii) sec A
(iii) cos2 A + sin2A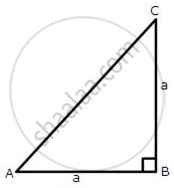
In the following figure:
AD ⊥ BC, AC = 26 CD = 10, BC = 42, ∠DAC = x and ∠B = y.
Find the value of :
(i) cot x
(ii) `1/sin^2 y – 1/tan^2 y`
(iii) `6/cos x – 5/cos y + 8 tan y`.
If 3 cos A = 4 sin A, find the value of :
(i) cos A(ii) 3 - cot2 A + cosec2A.
If sin A = cos A, find the value of 2 tan2A - 2 sec2 A + 5.
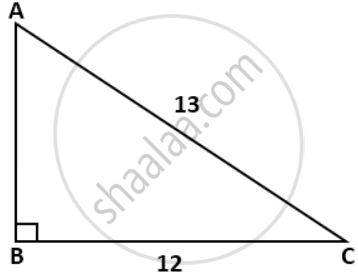
In the given figure, AC = 13cm, BC = 12 cm and ∠B = 90°. Without using tables, find the values of: sin A cos A