Advertisements
Advertisements
Question
Evaluate:
cos450 cos300 + sin450 sin300
Solution
On substituting the values of various T-ratios, we get:
cos450 cos300 + sin450 sin300
`=(1/sqrt(2) xxsqrt(3)/2 +1/sqrt(2) xx1/2) = (sqrt(3)/(2sqrt(2)) + 1/(2sqrt(2)) )= ((sqrt(3)+1)/(2sqrt(2)))`
APPEARS IN
RELATED QUESTIONS
If tan θ =`15/ 8 `, find the values of all T-ratios of θ.
If sin θ = `a/b`, show that `(sectheta + tan theta) = sqrt((b+a)/(b-a))`
In a ΔABC , ∠B = 90° , AB = 12 cm and BC = 5 cm Find
(i) cos A (ii) cosec A (iii) cos C (iv) cosec C
If A = 300 , verify that:
(iii) tan 2A = `(2tanA)/(1-tan^2A)`
Using the formula, sin A = `sqrt((1-cos 2A)/2) ` find the value of sin 300, it being given that cos 600 = `1/2`
If sin (A+B) = sin A cos B + cos A sin B and cos (A-B) = cos A cos B + sin A sin B
(i) sin (750)
(ii) cos (150)
If sec A = `sqrt2`, find the value of :
`(3cos^2"A"+5tan^2"A")/(4tan^4"A"–sin^2"A")`
From the following figure, find:
(i) y
(ii) sin x°
(iii) (sec x° - tan x°) (sec x° + tan x°)

Given : 17 cos θ = 15;
Find the value of: tan θ + 2 secθ .
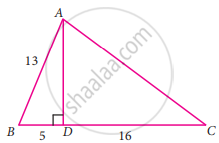
From the given figure, find the values of tan C