Question

In a ΔABC , ∠B = 90° , AB = 12 cm and BC = 5 cm Find
(i) cos A (ii) cosec A (iii) cos C (iv) cosec C

Answer 1

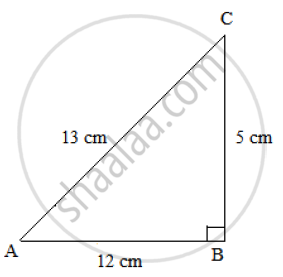
Using Pythagoras theorem, we get:
`AC^2 = AB^2 + BC^2`
`⟹ AC^2 = 12^2 + 5^2 = 144 + 25`
`⟹ AC^2 = 169`
⟹ 𝐴𝐶 = 13 𝑐𝑚
Now, for T-Ratios of ∠𝐴, 𝑏𝑎𝑠𝑒 = 𝐴𝐵 𝑎𝑛𝑑 𝑝𝑒𝑟𝑝𝑒𝑛𝑑𝑖𝑐𝑢𝑙𝑎𝑟 = 𝐵𝐶
(i)cos 𝐴 = `(AB)/(AC) = 12/13`

(ii) cosec A = `1/sin A=(AC)/(BC)=13/5`

Similarly, for T-Ratios of ∠𝐶, 𝑏𝑎𝑠𝑒 = 𝐵𝐶 𝑎𝑛𝑑 𝑝𝑒𝑟𝑝𝑒𝑛𝑑𝑖𝑐𝑢𝑙𝑎𝑟 = 𝐴𝐵
(iii)cos 𝐶 = `(BC)/(AC) = 5/13`

(iv) cosec C = `1/sin C=(AC)/(AB) = 13/12`