Advertisements
Advertisements
Question
Given: cos A = `( 5 )/ ( 13 )`
Evaluate:
- `(sin "A "–cot "A") / (2 tan "A")`
- `cot "A" + 1/cos"A"`
Solution
Consider the diagram below:
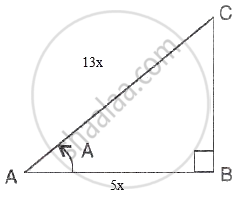
cos A = `( 5 )/( 13 )`
i.e. `"base"/"hypotenuse" = 5/13`
⇒ `"AB"/"AC" = 5/13`
Therefore, if length of AB = 5x, length of AC = 13x
Since
AB2 + BC2 = AC2 ...[Using Pythagoras Theroem]
(5x)2 + BC2 = (13x)2
BC2 = 169x2 – 25x2
BC2 = 144x2
∴ BC = 12x ...(perpendicular)
Now
tan A = `"perpendicular"/"base" = (12x)/(5x) = 12/5`
sin A = `"perpendicular"/"hypotenuse" = (12x)/(13x) = 12/13`
cot A = `"base"/"perpendicular" =(5x)/(12x) = 5/12`
(i) `(sin "A" – cot"A")/ (2tan "A")`
= `( 12 /13 – 5/12)/(2(12/5)`
= `(79)/(156). (5)/(24)`
= `( 395)/(3744 )`
(ii) cot A + `1/ cos "A"`
= `(5)/(12) + (1)/(5/13)`
= `(5)/(12) + (13)/(5)`
= `(181)/(60)`
APPEARS IN
RELATED QUESTIONS
If A = 30° B = 60° verify Sin (A + B) = Sin A Cos B + cos A sin B
Find acute angles A & B, if sin (A + 2B) = `sqrt3/2 cos(A + 4B) = 0, A > B`
If A, B, C are the interior angles of a ΔABC, show that `cos[(B+C)/2] = sin A/2`
If ∠A and ∠B are acute angles such that sin A = Sin B prove that ∠A = ∠B.
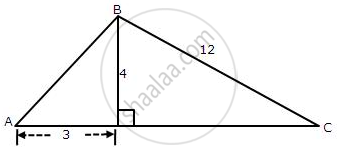
From the following figure, find the values of
(i) cos A
(ii) cosec A
(iii) tan2A - sec2A
(iv) sin C
(v) sec C
(vi) cot2 C - ` 1 / sin^2 "c"`
Given: sin θ = `p/q`.
Find cos θ + sin θ in terms of p and q.
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
tanB = `(8)/(15)`
In the given figure, PQR is a triangle, in which QS ⊥ PR, QS = 3 cm, PS = 4 cm and QR = 12 cm, find the value of: cot2P - cosec2P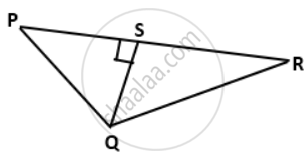
In the given figure, ΔABC is right angled at B.AD divides BC in the ratio 1 : 2. Find
(i) `("tan"∠"BAC")/("tan"∠"BAD")` (ii) `("cot"∠"BAC")/("cot"∠"BAD")`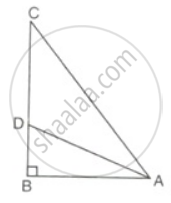
If A + B = 90°, cot B = `3/4` then tan A is equal to ______.
