If a = 600 and B = 300, Verify That: (Ii) Cos (A – B) = Cos a Cos B + Sin a Sin B - Mathematics

If A = 60⁰ and B = 30⁰, verify that:

(ii) cos (A – B) = cos A cos B + sin A sin B

cos (A – B) = cos 30^{0 =}`sqrt(3)/2`

cos A cos B + sin A sin B = cos 60⁰ cos 30⁰ + sin 60⁰ sin 30⁰

⁼`( 1/2 xx sqrt(3)/2 + sqrt(3)/2 xx1/2) = (sqrt(3)/4 + sqrt(3)/4) = 2 xx sqrt(3)/4 = sqrt(3)/2`

∴ cos (A – B) = cos A cos B + sin A sin B

shaalaa.com

Is there an error in this question or solution?

Chapter 6: T-Ratios of some particular angles - Exercises

Chapter 6 T-Ratios of some particular angles
Exercises | Q 15.2

Evaluate:
cos45⁰ cos30⁰ + sin45⁰ sin30⁰

Evaluate:
`(sin30°)/(cos 45°)+(cot45°)/(sec60° )- (sin60°)/(tan45°)+(cos30°)/(sin90°)`

Evaluate:

`2cos^2 60^0+3 sin^2 45^0 - 3 sin^2 30^0 + 2 cos^2 90 ^0`

If A = 60⁰ and B = 30⁰, verify that:

cos (A + B) = cos A cos B - sin A sin B

In the adjoining figure, ΔABC is right-angled at B and ∠A = 45⁰. If AC = 3`sqrt(2)`cm, find (i) BC, (ii) AB.

If sin (A + B) = 1 and cos (A – B) = 1, 0⁰ ≤ (A + B) ≤ 90⁰ and A > B, then find A and B.

In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.

cotA = `(1)/(11)`

In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.

cose C = `(15)/(11)`

In ΔABC, ∠B = 90°. If AB = 12units and BC = 5units, find: cos C

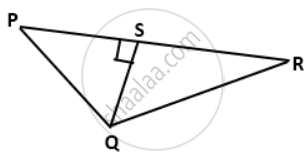
In the given figure, PQR is a triangle, in which QS ⊥ PR, QS = 3 cm, PS = 4 cm and QR = 12 cm, find the value of: sin P