Advertisements
Advertisements
Question
If sin (A + B) = 1 and cos (A – B) = 1, 00 ≤ (A + B) ≤ 900 and A > B, then find A and B.
Solution
Here, sin (A + B) = 1
⇒ sin (A + B) = 900 [∵ sin 900 = 1]
⇒ (A + B) = 900 …….(i)
Also, cos (A – B) = 1
⇒ cos (A – B) = 00 [∵ cos 00 = 1]
⇒ A – B = 00 ….(ii)
Solving (i) and (ii), we get:
A = 450 and B = 450
APPEARS IN
RELATED QUESTIONS
If `sin (A – B) = 1/2` and `cos (A + B) = 1/2`, `0^@` < A + `B <= 90^@`, A > B Find A and B.
If sec `theta = 17/8 ` verify that `((3-4sin^2theta)/(4 cos^2theta -3))=((3-tan^2theta)/(1-tan^2theta))`
If x = cosec A +cos A and y = cosec A – cos A then prove that `(2/(x+y))^2 + ((x-y)/2)^2` = 1
Evaluate:
cos600 cos300− sin600 sin300
In the adjoining figure, ΔABC is right-angled at B and ∠A = 300. If BC = 6cm, find (i) AB, (ii) AC.
In the given figure, PQR is a triangle, in which QS ⊥ PR, QS = 3 cm, PS = 4 cm and QR = 12 cm, find the value of: sin P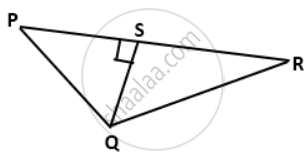
If cosec θ = `(29)/(20)`, find the value of: cosec θ - `(1)/("cot" θ)`
From the given figure, find all the trigonometric ratios of angle B
From the given figure, find the values of tan C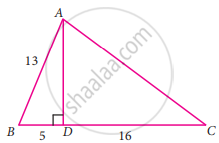
Evaluate: `5/(cot^2 30^circ) + 1/(sin^2 60^circ) - cot^2 45^circ + 2 sin^2 90^circ`.
