Advertisements
Advertisements
Question
If `sin (A – B) = 1/2` and `cos (A + B) = 1/2`, `0^@` < A + `B <= 90^@`, A > B Find A and B.
Solution
`sin (A – B) = 1/2` and `cos (A + B) = 1/2`
Now `sin (A - B) = 1/2`
`=> sin (A- B) = sin 30^@`
`=> A - B( = 30^@` ....(1)
And `cos (A + B) = 1/2`
`=> cos (A + B) = cos 60^@`
`=> A + B = 60^@` ...(2)
Adding (1) and (2) we get
`2A = 90^@`
`=> A = 90^@/2 = 45^@`
Put `A = 45^@` in (2 ) we get
`=> 45^@ + B = 60^@`
`=> B = 60^@ - 45^@``
`=>B = 15^@`
Thus `A = 45^@ and B = 15^@`
RELATED QUESTIONS
If 3cos θ – 4sin = 2cos θ + sin θ Find tan θ.
In right angled triangle ΔABC at B, ∠A = ∠C. Find the values of Sin A cos C + Cos A Sin C
If sin θ = `a/b`, show that `(sectheta + tan theta) = sqrt((b+a)/(b-a))`
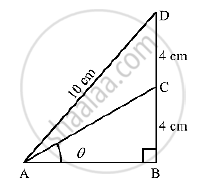
In the adjoining figure, `∠B = 90° , ∠BAC = theta° , BC = CD = 4cm and AD = 10 cm`. find (i) sin theta and (ii) `costheta`
If A = 300 , verify that:
(ii) cos 2A = `(1- tan^2A)/(1+tan^2A)`
Using the formula, tan 2A =`(2 tan A )/(1- tan^2 A)` find the value of tan 600, it being given that tan 300 = `1/sqrt(3)`.
If sinA = 0.8, find the other trigonometric ratios for A.
In the given figure, AC = 13cm, BC = 12 cm and ∠B = 90°. Without using tables, find the values of: sin A cos A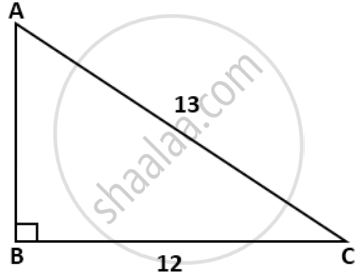
If cos θ : sin θ = 1 : 2, then find the value of `(8costheta - 2sintheta)/(4costheta + 2sintheta`
From the given figure, prove that θ + ∅ = 90°. Also prove that there are two other right angled triangles. Find sin α, cos β and tan ∅
