Advertisements
Advertisements
Question
If cos θ : sin θ = 1 : 2, then find the value of `(8costheta - 2sintheta)/(4costheta + 2sintheta`
Solution
cos θ : sin θ = 1 : 2
The value of `(8costheta - 2sintheta)/(4costheta + 2sintheta`
= `(8(sintheta/2) - 2sintheta)/(4(sintheta/2) + 2sintheta)`
= `(4 sintheta - 2 sintheta)/(2 sintheta + 2 sintheta)`
= `(2 sintheta)/(4 sintheta)`
= `2/4`
= `1/2`
Aliter:
cos θ : sin θ = 1 : 2
cos θ = sin θ
⇒ 2 = `sintheta/costheta`
⇒ 2 = tan θ
AC = `sqrt(1^2 + 2^2)`
= `sqrt(1 + 4)`
⇒ `sqrt(5)`
∴ sin θ = `2/sqrt(5)`, cos θ = `1/sqrt(5)`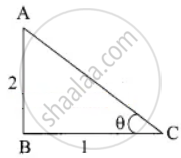
The value of `(8 cos theta - 2 sin theta)/(4 cos theta + 2 sin theta)`
= `8(1/sqrt(5)) - 2(2/sqrt(5)) ÷ 4(1/sqrt(5)) + 2 xx (2/sqrt(5))`
= `(8/sqrt(5)) - (4/sqrt(5)) ÷ (4/sqrt(5)) + (4/sqrt(5))`
= `((8 - 4)/sqrt(5)) ÷ ((4 + 4)/sqrt(5))`
= `(4/sqrt(5)) ÷ (8/sqrt(5))`
= `(4/sqrt(5)) xx (sqrt(5)/8)`
= `(4/8)`
= `1/2`
∴ The value is `1/2`
APPEARS IN
RELATED QUESTIONS
In right angled triangle ΔABC at B, ∠A = ∠C. Find the values of Sin A cos C + Cos A Sin C
If tan θ = `4/3`, show that `(sintheta + cos theta )=7/5`
Evaluate:
sin600 cos300 + cos600 sin300
Show that:
(ii) `(cos30^0+sin 60^0)/(1+sin30^0+cos60^0)=cos 30^0`
If A and B are acute angles such that tan A =`1/3, tan B = 1/2 and tan (A + B) =` show that `A+B = 45^0`
If tan A + cot A = 5;
Find the value of tan2 A + cot2 A.
Given : 17 cos θ = 15;
Find the value of: tan θ + 2 secθ .
In the given figure; ∠C = 90o and D is mid-point of AC.
Find :
(i) `(tan∠CAB)/ (tan∠CDB)` (ii) `(tan∠ABC)/ (tan∠DBC)`
In ΔABC, ∠B = 90°. If AB = 12units and BC = 5units, find: cot C
If cos A = `(2x)/(1 + x^2)`, then find the values of sin A and tan A in terms of x
