Advertisements
Advertisements
Question
If A and B are acute angles such that tan A =`1/3, tan B = 1/2 and tan (A + B) =` show that `A+B = 45^0`
Solution
Given:
tan A = `1/3 and tan B = 1/2`
tan (A+B) = `(tan A + tan B)/(1- tan A tan B)`
On substituting these values in RHS of the expression, we get:
`(tan A + tan B )/(1- tan A tan B) = ((1/3 +1/2))/((1-1/3xx1/3)` =`((5/6))/(1-1/6) = ((5/6))/((5/6))=1`
⇒ tan (A + B) = 1= tan `45^0` [ ∵ tan 450 =1]
∴ A+B = 450
APPEARS IN
RELATED QUESTIONS
If sin θ = cos (θ – 45°), where θ – 45° are acute angles, find the degree measure of θ
If tan θ = `1/sqrt(7) `show that ` (cosec ^2 θ - sec^2 θ)/(cosec^2 θ + sec^2 θ ) = 3/4`
`(cos 28°)/(sin 62°)` = ?
From the following figure, find the values of
(i) cos A
(ii) cosec A
(iii) tan2A - sec2A
(iv) sin C
(v) sec C
(vi) cot2 C - ` 1 / sin^2 "c"`
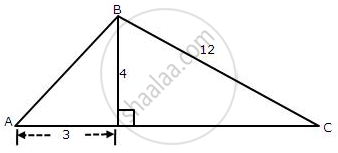
In ΔABC, ∠A = 90°. If AB = 5 units and AC = 12 units, find: cos C
If cosB = `(1)/(3)` and ∠C = 90°, find sin A, and B and cot A.
In the given figure, PQR is a triangle, in which QS ⊥ PR, QS = 3 cm, PS = 4 cm and QR = 12 cm, find the value of: cot2P - cosec2P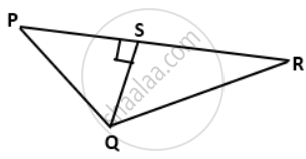
In the given figure, ΔABC is right angled at B.AD divides BC in the ratio 1 : 2. Find
(i) `("tan"∠"BAC")/("tan"∠"BAD")` (ii) `("cot"∠"BAC")/("cot"∠"BAD")`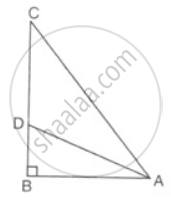
In the given figure, AC = 13cm, BC = 12 cm and ∠B = 90°. Without using tables, find the values of: sin A cos A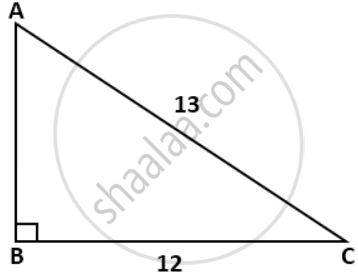
From the given figure, prove that θ + ∅ = 90°. Also prove that there are two other right angled triangles. Find sin α, cos β and tan ∅
