Advertisements
Advertisements
Question
`(cos 28°)/(sin 62°)` = ?
Options
2
-1
0
1
Solution
1
Explanation:
`[cos 28°]/[sin 62°]`
= `[sin( 90°- 28°)]/(sin 62°)` ...[cos θ = sin(90°- θ)]
= `[sin 62°]/[sin 62°]`
= 1
APPEARS IN
RELATED QUESTIONS
In a ΔABC, right angled at A, if tan C = `sqrt3` , find the value of sin B cos C + cos B sin C.
If sin θ ,` sqrt (3)/2` find the value of all T- ratios of θ .
If cot θ = 2 find all the values of all T-ratios of θ .
If tan θ = `1/sqrt(7) `show that ` (cosec ^2 θ - sec^2 θ)/(cosec^2 θ + sec^2 θ ) = 3/4`
If cosec θ = `sqrt5`, find the value of:
- 2 - sin2 θ - cos2 θ
- 2 + `1/sin^2"θ" – cos^2"θ"/sin^2"θ"`
In triangle ABC, AD is perpendicular to BC. sin B = 0.8, BD = 9 cm and tan C = 1.
Find the length of AB, AD, AC, and DC.
If cosec A + sin A = 5`(1)/(5)`, find the value of cosec2A + sin2A.
In the given figure, AD is the median on BC from A. If AD = 8 cm and BC = 12 cm, find the value of cos y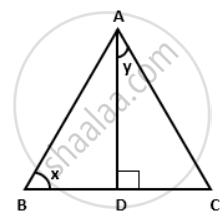
In the given figure, ΔABC is right angled at B.AD divides BC in the ratio 1 : 2. Find
(i) `("tan"∠"BAC")/("tan"∠"BAD")` (ii) `("cot"∠"BAC")/("cot"∠"BAD")`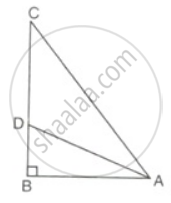
Statement A (Assertion): For 0 < θ ≤ 90°, cosec θ – cot θ and cosec θ + cot θ are reciprocal of each other.
Statement R (Reason): cosec2 θ – cot2 θ = 1
