Advertisements
Advertisements
Question
In a ΔABC, right angled at A, if tan C = `sqrt3` , find the value of sin B cos C + cos B sin C.
Solution
In a Δle ABC right angled at A tan C = `sqrt3`
Find sin B cos C + cos B sin C
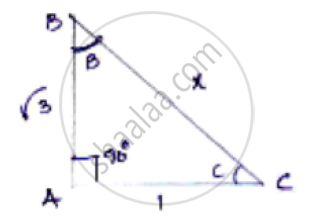
`tan c = sqrt3`
`tan c = "oppoite side"/"adjacent side"`
Let x be the hypotenuse By applying Pythagoras we get
`BC^2 = BA^2 + AC^2`
`x^2 = (sqrt3)^2 + 1^2`
x2 = Δ ⇒ x = 2
At ∠B, `sin B = (AC)/(BC) = 1/2`
`cos B = sqrt3/2`
At ∠C, `sin = sqrt3/2`
`cos c = 1/2`
On substitution we get
`=> 1/2 xx 1/2 + sqrt3/2 xx sqrt3/2`
`=> 1/4 + (sqrt3)/4 xx (sqrt3) = (sqrt3 xx sqrt3 + 1)/4 = (3 + 1)/4 = 4/4 = 1`
APPEARS IN
RELATED QUESTIONS
If A = B = 60°. Verify `tan (A - B) = (tan A - tan B)/(1 + tan tan B)`
In right angled triangle ABC. ∠C = 90°, ∠B = 60°. AB = 15 units. Find remaining angles and sides.
If cos θ = `7/25` find the value of all T-ratios of θ .
In the figure of ΔPQR , ∠P = θ° and ∠R =∅° find
(i) `sqrt(X +1) cot ∅`
(ii)`sqrt( x^3 + x ^2) tantheta`
(iii) cos θ

Evaluate:
cos600 cos300− sin600 sin300
Evaluate:
cos450 cos300 + sin450 sin300
Given q tan A = p, find the value of:
`("p" sin "A" – "q" cos "A")/("p" sin "A" + "q" cos "A")`.
In the given figure, PQR is a triangle, in which QS ⊥ PR, QS = 3 cm, PS = 4 cm and QR = 12 cm, find the value of: cot2P - cosec2P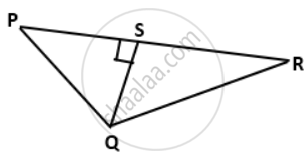
From the given figure, find the values of sec B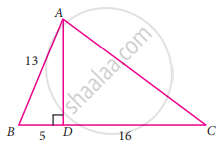
If 3 cot A = 2, then find the value of `(4sin"A" - 3cos"A")/(2sin"A" + 3cos"A")`
