Advertisements
Advertisements
Question
Given q tan A = p, find the value of:
`("p" sin "A" – "q" cos "A")/("p" sin "A" + "q" cos "A")`.
Solution
q tan A = p
tan A = `"P"/"q"`
Let P = P & B = q
H2 = P2 + B2
H2 = P2 + q2
H = `sqrt(p^2+q^2)`
`("p" sin "A" – "q" cos "A")/("p" sin "A" + "q" cos "A")`
= `("p sinA"/cos "A" – "q cos A"/cos"A")/("p sin A"/cos "A" + "q cos A"/cos"A")`
= `("p"tan"A" – "q")/ ("p" tan "A" + "q")`
= `("p"(p/q) – "q")/("p"(p/q) + "q")`
= `(("p"^2 – "q"^2)/("q"))/(("p"^2 + "q"^2)/("q"))`
= `("p"^2 – "q"^2)/("p"^2 + "q"^2)`
APPEARS IN
RELATED QUESTIONS
In ∆PQR, right-angled at Q, PQ = 3 cm and PR = 6 cm. Determine ∠P and ∠R.
If tan θ =`15/ 8 `, find the values of all T-ratios of θ.
If cosec θ = `sqrt(10)` find all the values of all T-ratios of θ
If tan θ = `1/sqrt(7) `show that ` (cosec ^2 θ - sec^2 θ)/(cosec^2 θ + sec^2 θ ) = 3/4`
Evaluate:
`(5 cos^2 60^circ + 4 sec^2 30^circ - tan^2 45^circ)/(sin^2 30^circ + cos^2 30^circ)`
In the adjoining figure, ΔABC is a right-angled triangle in which ∠B = 900, ∠300 and AC = 20cm. Find (i) BC, (ii) AB.
In triangle ABC, AD is perpendicular to BC. sin B = 0.8, BD = 9 cm and tan C = 1.
Find the length of AB, AD, AC, and DC.
From the given figure, find the values of sin B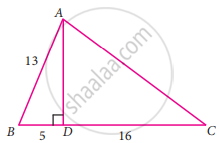
From the given figure, find the values of sec B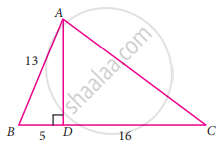
From the given figure, prove that θ + ∅ = 90°. Also prove that there are two other right angled triangles. Find sin α, cos β and tan ∅
