Advertisements
Advertisements
Question
From the given figure, find the values of sec B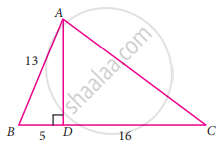
Solution
In the right ΔABD,
AD2 = AB2 – BD2
= 132 – 52
= 169 – 25
= 144
AD = `sqrt(144)`
= 12
In the right ΔADC,
AC2 = AD2 + DC2
= 122 + 162
= 144 + 256
= 400
AC = `sqrt(400)`
= 20
sec B = `"hypotenuse"/"adjacent side" = "AB"/"BD" = 13/5`
APPEARS IN
RELATED QUESTIONS
If 8 tan A = 15, find sin A – cos A.
If A = B = 60°, verify that sin (A − B) = sin A cos B − cos A sin B
If tan θ =`15/ 8 `, find the values of all T-ratios of θ.
If sin θ = ` (a^2 - b^2)/(a^2+b^2)`find all the values of all T-ratios of θ .
If 3 cot `theta = 2, `show that `((4 sin theta - 4 cos theta))/((2 sin theta + 6 cos theta ))=1/3`
In ΔABC , ∠C = 90° ∠ABC = θ° BC = 21 units . and AB= 29 units. Show thaT `(cos^2 theta - sin^2 theta)=41/841`
If x = cot A + cos A and y = cot A – cos A then prove that `((x-y)/(x+y))^2 + ((x-y)/2)^2=1`
In triangle ABC, AD is perpendicular to BC. sin B = 0.8, BD = 9 cm and tan C = 1.
Find the length of AB, AD, AC, and DC.
In the given figure, AD is the median on BC from A. If AD = 8 cm and BC = 12 cm, find the value of tan x. cot y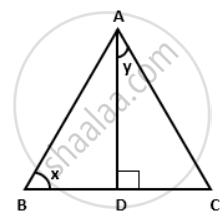
Evaluate: `5/(cot^2 30^circ) + 1/(sin^2 60^circ) - cot^2 45^circ + 2 sin^2 90^circ`.
